题目内容
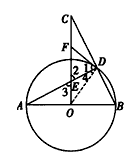
如图,AB为⊙O的直径,D是⊙O上的一点,过O点作AB的垂线交AD于点E,交BD的延长线于点C,F为CE上一点,且FD=FE。
(1)请探究FD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,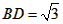 ,求BC的长。
,求BC的长。
(1)请探究FD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,
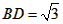 ,求BC的长。
,求BC的长。
| 解:(1) FD与⊙O相切,理由如下: 连接OD,如图所示, ∵OC⊥AB, ∴∠AOC=90°, ∴∠3+∠A=90°, ∵FE=FD, ∴∠1=∠2, 又∵∠2=∠3, ∴∠1=∠3, 又∵OA=OD, ∴∠A=∠4, ∴∠1+∠4=90°, ∴FD与⊙O相切; |
 |
| (2)∴⊙O的半径为2, ∴OB=2,AB=4, 又∵AB是⊙O的直径, ∴∠ADB=90°, ∵OC⊥ AB, ∴∠ADB=∠BOC=90°, 又∵∠B=∠B, ∴Rt△ABD∽Rt△CBO, ∴ 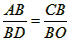 即 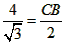 , ,∴ 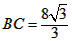 。 。 |

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )| A、1cm | B、2cm | C、3cm | D、4cm |
 如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为