题目内容
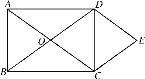
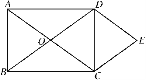
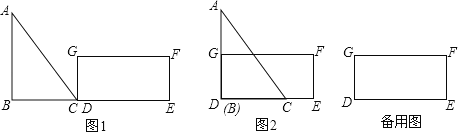
【题目】如图1，已知△ABC中，∠B=90°，AB=BC=4cm，长方形DEFG中，DE=6cm，DG=2cm，点B、C、D、E在同一条直线上，开始时点C与点D重合，然后△ABC沿直线BE以每秒1cm的速度向点E运动，运动时间为t秒，当点B运动到点E时运动停止．（友情提示：长方形的对边平行，四个内角都是直角．）
（1）直接填空：∠BAC=_________度，
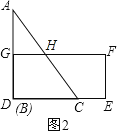
（2）当t为何值时，AB与DG重合（如图2所示），并求出此时△ABC与长方形DEFG重合部分的面积．
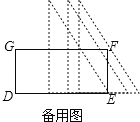
（3）探索：当6≤t≤8时，△ABC与长方形DEFG重合部分的图形的内角和的度数（直接写出结论及相应的t值，不必说明理由）．
【答案】（1）45°（2）6 cm2（3）当t=6时，重合部分为四边形，内角和为360°，当6＜t＜8时重合部分为五边形，内角和为540°，当t=8时，重合部分为四边形，内角和为360°．
【解析】
试题分析：（1）根据等腰直角三角形的性质可得∠BAC=45°；
（2）首先计算出GH的长，再利用梯形的面积公式可直接得到答案；
（3）根据题意画出图形可直接看出重合部分是哪种多边形，进而得到答案．
解：（1）在△ABC中，
∵∠B=90°，AB=BC，
∴∠BAC=45°，
故答案为：45°；
（2）由题意CD=BC=4cm，
4÷1=4（秒），
长方形DEFG中，GF∥DE，∠D=90°，
∴∠AGH=∠D=90°，
由（1）得∠BAC=45°，
∴∠AHG=180°﹣∠BAC﹣∠AGH=45°，
∴∠BAC=∠AHG，
∴GH=AG，
∵AG=AD﹣GD=4﹣2=2cm，
∴GH=2cm，
∴S梯形GDCH=
（cm2）；
（3）如图所示：当t=6时，重合部分为四边形，内角和为360°，
当6＜t＜8时重合部分为五边形，内角和为540°，
当t=8时，重合部分为四边形，内角和为360°．
