题目内容
 如图,直线AB、CD相交于点O,∠AOD=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么秒钟后⊙P与直线CD相切.
如图,直线AB、CD相交于点O,∠AOD=30°,半径为1cm的⊙P的圆心在射线OA上,且与点O的距离为6cm.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么秒钟后⊙P与直线CD相切.
- A.4
- B.8
- C.4或6
- D.4或8
D
分析:由题意判定CD是圆的切线,从其性质在△P1EO中求得OP1,从而求得.
解答:①由题意CD与圆P1相切于点E,
∴P1E⊥CD
又∵∠AOD=30°,r=1cm
∴在△OEP1中OP1=2cm
又∵OP=6cm
∴P1P=4cm
∴圆P到达圆P1需要时间为:4÷1=4(秒),
②当圆心P在直线CD的右侧时,
PP2=6+2=8cm,
∴圆P到达圆P2需要时间为:8÷1=8(秒),
综上可知:⊙P与直线CD相切时,时间为4或8秒钟,
故选D.
点评:本题考查了切线的判定和性质,从切线入手从而解得.
分析:由题意判定CD是圆的切线,从其性质在△P1EO中求得OP1,从而求得.
解答:①由题意CD与圆P1相切于点E,
∴P1E⊥CD
又∵∠AOD=30°,r=1cm
∴在△OEP1中OP1=2cm
又∵OP=6cm
∴P1P=4cm
∴圆P到达圆P1需要时间为:4÷1=4(秒),
②当圆心P在直线CD的右侧时,
PP2=6+2=8cm,
∴圆P到达圆P2需要时间为:8÷1=8(秒),
综上可知:⊙P与直线CD相切时,时间为4或8秒钟,
故选D.
点评:本题考查了切线的判定和性质,从切线入手从而解得.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 21、如图,直线AB、CD、EF都经过点O,且AB⊥CD,∠COE=35°,求∠DOF、∠BOF的度数.
21、如图,直线AB、CD、EF都经过点O,且AB⊥CD,∠COE=35°,求∠DOF、∠BOF的度数.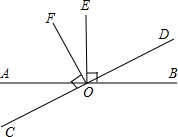 如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD.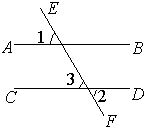 25、完成推理填空:如图:直线AB、CD被EF所截,若已知AB∥CD,
25、完成推理填空:如图:直线AB、CD被EF所截,若已知AB∥CD, 如图,直线AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=24°,∠COG的度数=
如图,直线AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=24°,∠COG的度数= 如图,直线AB,CD相交于O点,EO⊥CD,垂足为O点,若∠BOE=50°,求∠AOD的度数.
如图,直线AB,CD相交于O点,EO⊥CD,垂足为O点,若∠BOE=50°,求∠AOD的度数.