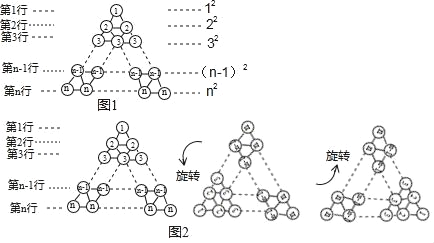
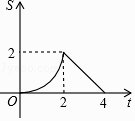
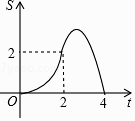
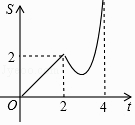
��Ŀ����
����Ŀ��Ϊ�������ݹʻƺӷ�����һ�γ�Ϊ360�ĺӵ����������ɼס����������̶ӽ�����ɣ�����ʱ20�죮��֪��ÿ������24�ף��Ҷ�ÿ������16�ף�
��1���������⣬С����С���ֱ��г����µ�һԪһ�η��̣��в���������
����24x+16�� ��=360��
����![]() ��
��
��ֱ�ָ������������x�����壬����ȫ���̣�
С����x��ʾ���� ����
С����x��ʾ���� ����
��2����ס������ӷֱ����κӵ������ף���д�������Ľ����̣�
���𰸡���1��20��x��360��x���ӹ�����ʱ�䣬�����κӵ��ij��ȣ���2���ס������ӷֱ����κӵ�120�ף�240�ף�
��������
��1���������з��̿ɵõ�һ������Ϊ24x+16��20-x��=360��x��ʾ���Ǽӹ�����ʱ�䣬�ڶ�������Ϊ![]() x��ʾ���Ǽ����κӵ��ij��ȣ�
x��ʾ���Ǽ����κӵ��ij��ȣ�
��2�����ڶ������̼��ɣ�
(1)�������,��һ������Ϊ24x+16(20x)=360��
x��ʾ���Ǽӹ�����ʱ�䣬
�ڶ�������Ϊ![]()
x��ʾ���Ǽ����κӵ��ij��ȣ�
�ʴ�Ϊ��20x��360x���ӹ�����ʱ�䣬�����κӵ��ij��ȣ�
(2)������κӵ��ij���Ϊx�ף�
�з��̵ã�![]()
��ã�x=120��
��360x=360120=240.
�𣺼ס������ӷֱ����κӵ�120�ף�240��.

 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�����Ŀ����������������˾������һ���ļ���װ��ͨ��ʵ���̵�������̵�����;���������ۣ�����һ��ʱ��ù�˾��������Ʒ�����������������Ϊ��30��ĸ��ٵ��飬����ʵ���̵����������y1���ټ�����ʱ��t��tΪ��������λ���죩�IJ��ֶ�Ӧֵ���±���ʾ�������̵����������y2���ټ�����ʱ��t��tΪ��������λ���죩�IJ��ֶ�Ӧֵ��ͼ��ʾ��
ʱ��t���죩 | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
�������� | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
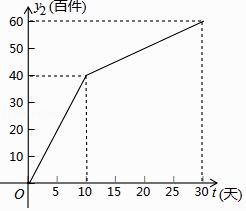
��1��������һ�κ��������κ����ͷ����������У�ѡ����ʵĺ����ܷ�ӳy1��t�ı仯���ɣ������y1��t�ĺ�����ϵʽ���Ա���t��ȡֵ��Χ��
��2����y2��t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
��3���ڸ��ٵ����30���У���ʵ���̵�������̵������������Ϊy���ټ�������y��t�ĺ�����ϵʽ����tΪ��ֵʱ������������y�ﵽ��������ʱ�����ֵ��