题目内容
如图,在直角坐标系中,O为原点,A(4,12)为双曲线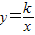 (x>0)上的一点.
(x>0)上的一点.(1)求k的值;
(2)过双曲线上的点P作PB⊥x轴于B,连接OP,若Rt△OPB两直角边的比值为
 ,试求点P的坐标;
,试求点P的坐标;(3)分别过双曲线上的两点P1、P2,作P1B1⊥x轴于B1,P2B2⊥x轴于B2,连接OP1、OP2.设Rt△OP1B1、Rt△OP2B2的周长分别为l1、l2,内切圆的半径分别为r1、r2,若
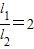 ,试求
,试求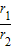 的值.
的值.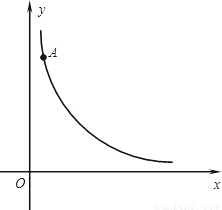
【答案】分析:(1)直接把A的坐标代入解析式中就可以确定k的值;
(2)设P(m,n),根据函数解析式和Rt△OPB两直角边的比值可以列出方程,解方程可以求出m,n,也就求出了点P的坐标;
(3)根据最下图此题首先应该知道一个结论: (a+b+c)•r=
(a+b+c)•r= ab,利用这个结论可以得到
ab,利用这个结论可以得到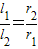 ,这样就可以求出
,这样就可以求出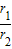 的值了.
的值了.
解答: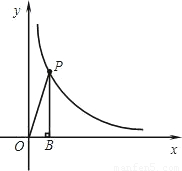 解:(1)将A(4,12)代入双曲线
解:(1)将A(4,12)代入双曲线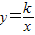 中,得12=
中,得12=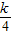 ,则k=48;(3分)
,则k=48;(3分)
(2)由(1)得双曲线解析式为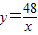 ,(4分)
,(4分)
设P(m,n),∴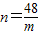 ,即mn=48,(5分)
,即mn=48,(5分)
当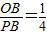 时,即
时,即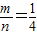 ,可设m=z,n=4z,
,可设m=z,n=4z,
∴z•4z=48,解得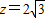 ,
,
∴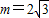 ,
,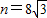 ,
,
∴P(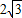 ,
,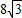 ),(7分)
),(7分)
当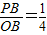 时,同理可求得P(
时,同理可求得P(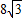 ,
,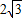 );(8分)
);(8分)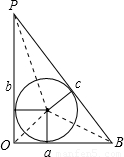
(3)在Rt△OP1B1中,设OB1=a1,P1B1=b1,OP1=c1,
则P1(a1,b1),由(2)得a1b1=48,
在Rt△OP2B2中,设OB2=a2,P2B2=b2,OP2=c2,
则P2(a2,b2),由(2)得a2b2=48,
∵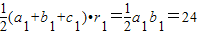
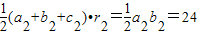 (10分)
(10分)
∴(a1+b1+c1)•r1=(a2+b2+c2)•r2(11分)
即l1•r1=l2•r2,故 (12分)
(12分)
又∵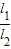 =2,∴
=2,∴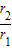 =2,即得:
=2,即得: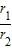 =
= .(13分)
.(13分)
点评:此题主要考查了利用反比例函数的图象和性质解题,也利用了三角形的内切圆的知识,有一定综合性.
(2)设P(m,n),根据函数解析式和Rt△OPB两直角边的比值可以列出方程,解方程可以求出m,n,也就求出了点P的坐标;
(3)根据最下图此题首先应该知道一个结论:
 (a+b+c)•r=
(a+b+c)•r= ab,利用这个结论可以得到
ab,利用这个结论可以得到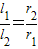 ,这样就可以求出
,这样就可以求出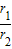 的值了.
的值了.解答:
 解:(1)将A(4,12)代入双曲线
解:(1)将A(4,12)代入双曲线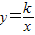 中,得12=
中,得12=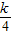 ,则k=48;(3分)
,则k=48;(3分)(2)由(1)得双曲线解析式为
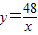 ,(4分)
,(4分)设P(m,n),∴
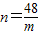 ,即mn=48,(5分)
,即mn=48,(5分)当
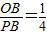 时,即
时,即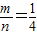 ,可设m=z,n=4z,
,可设m=z,n=4z,∴z•4z=48,解得
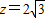 ,
,∴
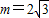 ,
,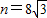 ,
,∴P(
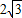 ,
,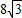 ),(7分)
),(7分)当
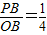 时,同理可求得P(
时,同理可求得P(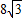 ,
,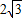 );(8分)
);(8分)
(3)在Rt△OP1B1中,设OB1=a1,P1B1=b1,OP1=c1,
则P1(a1,b1),由(2)得a1b1=48,
在Rt△OP2B2中,设OB2=a2,P2B2=b2,OP2=c2,
则P2(a2,b2),由(2)得a2b2=48,
∵
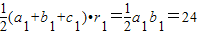
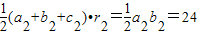 (10分)
(10分)∴(a1+b1+c1)•r1=(a2+b2+c2)•r2(11分)
即l1•r1=l2•r2,故
 (12分)
(12分)又∵
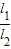 =2,∴
=2,∴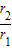 =2,即得:
=2,即得: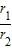 =
= .(13分)
.(13分)点评:此题主要考查了利用反比例函数的图象和性质解题,也利用了三角形的内切圆的知识,有一定综合性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: