Question

【题目】如图，已知AB∥CD，C在D的右侧，BE平分∠ABC，DE平分∠ADC，BE、DE所在直线交于点E．∠ADC =70°.

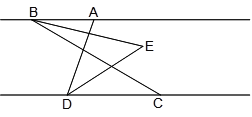
（1）求∠EDC的度数；

（2）若∠ABC =n°，求∠BED的度数（用含n的代数式表示）；

（3）将线段BC沿DC方向平移， 使得点B在点A的右侧，其他条件不变，画出图形并判断∠BED的度数是否改变，若改变，求出它的度数（用含n的式子表示），不改变，请说明理由.

Answer 1

【答案】(1)、35°；(2)、(n+35)°；(3)、(215－n)°.

【解析】

试题分析：(1)、根据角平分线直接得出答案；(2)、过点E作EF∥AB，然后根据平行线的性质和角平分线的性质求出角度；(3)、首先根据题意画出图形，然后过点E作EF∥AB，按照第二小题同样的方法进行计算角度.

试题解析：(1)、∵DE平分∠ADC，∠ADC=70°，∴∠EDC=∠ADC=×70°=35°；

(2)、过点E作EF∥AB，

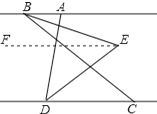
∵AB∥CD， ∴AB∥CD∥EF， ∴∠ABE=∠BEF，∠CDE=∠DEF，

∵BE平分∠ABC，DE平分∠ADC，∠ABC=n°，∠ADC=70°，

∴∠ABE=∠ABC=n°，∠CDE=∠ADC=35°， ∴∠BED=∠BEF+∠DEF=n°+35°；

(3)、过点E作EF∥AB

∵BE平分∠ABC，DE平分∠ADC，∠ABC=n°，∠ADC=70° ∴∠ABE=∠ABC=n°，∠CDE=∠ADC=35°

∵AB∥CD，∴AB∥CD∥EF， ∴∠BEF=180°-∠ABE=180°-n°，∠CDE=∠DEF=35°，

∴∠BED=∠BEF+∠DEF=180°-n°+35°=215°-n°.