题目内容
等腰梯形的一腰长为2cm，上底长为5cm，一个钝角是120°，该梯形的周长等于______．
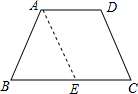
如图，过点A作AE∥CD，交BC于点E，
∵等腰梯形ABCD中，AD∥BC，AB=CD=2cm，
∴四边形AECD是平行四边形，
∴CE=AD=5cm，AE=CD，
∴AB=AE，
∵∠BAD=120°，
∴∠B=180°-∠BAD=60°，
∴△ABE是等边三角形，
∴BA=AB=2cm，
∴BC=BE+CE=2+5=7（cm），
∴该梯形的周长等于：AB+BC+CD+AD=2+7+2+5=16（cm）．
故答案为：16cm．
∵等腰梯形ABCD中，AD∥BC，AB=CD=2cm，
∴四边形AECD是平行四边形，
∴CE=AD=5cm，AE=CD，
∴AB=AE，
∵∠BAD=120°，
∴∠B=180°-∠BAD=60°，
∴△ABE是等边三角形，
∴BA=AB=2cm，
∴BC=BE+CE=2+5=7（cm），
∴该梯形的周长等于：AB+BC+CD+AD=2+7+2+5=16（cm）．
故答案为：16cm．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
