题目内容
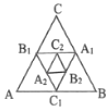
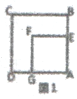
【题目】发现来源于探究。小亮进行数学探究活动,作边长为a的正方形ABCD和边长边b的正方形AEFG(a>b),开始时点E在AB上,如图1,将正方形AEFG绕点A逆时针方向旋转。
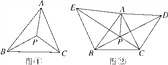
(1)如图2,小亮将正方形AEFG绕点A顺时针方向旋转,连接BE、DG,请证明:△ADG≌△ABE;
(2)如图3,小亮将正方形AEFG绕点A顺时针方向旋转,连接BE、DG,当点G恰好落在线段BE上,且a=3,b=2时,请你帮他求此时DG的长。
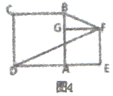
(3)如图4,小亮旋转正方形AEFG,当点E在DA的延长线上时,连接BF、DF,若FG平分∠BFD,请你帮他求a:b的值.


【答案】(1)见解析;(2)DG=![]() +
+![]() ;(3)a:b=
;(3)a:b=![]() :1.
:1.
【解析】分析:(1)如图2中,根据![]() 即可判定
即可判定![]() ≌
≌![]()
![]() 连接
连接![]() ,根据
,根据![]() ≌
≌![]() 得到
得到![]() 证明
证明![]() 为直角三角形, 设
为直角三角形, 设![]() 则
则![]() 根据
根据![]() 列出方程求解即可.
列出方程求解即可.
![]() 设
设![]() 交
交![]() 于M,证明
于M,证明![]() ,根据相似三角形的性质,即可求出
,根据相似三角形的性质,即可求出
![]() 的值.
的值.
详解:(1)∵四边形![]() 和四边形
和四边形![]() 为正方形,
为正方形,
∴![]()
∴![]()
即![]() ,
,
∴![]() ≌
≌![]()
(2)连接![]() ,由(1)可知,
,由(1)可知,![]() ≌
≌![]() 因此
因此![]()
∵四边形![]() 和四边形
和四边形![]() 为正方形,
为正方形,
![]()
∴![]()
∴![]() 为直角三角形,
为直角三角形,
设![]() 则
则![]()
∵![]()
![]()
解得:![]()
![]() (不合题意,舍去)
(不合题意,舍去)
因此:![]()
(3)设![]() 交
交![]() 于M,
于M,
∵四边形![]() 和四边形
和四边形![]() 为正方形,
为正方形,
∴![]()
∴![]()
∵FG平分![]()
∴![]()
又![]()
∴![]() ≌
≌![]()
∴![]()
∴![]()
∵![]()
∴![]() ,
,
∴![]()
∴![]() ,
,
解得![]()
![]()
∴![]()

练习册系列答案
相关题目