题目内容
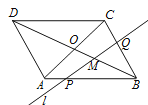
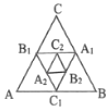
【题目】如图，点A1、B1、C1分别为△ABC的边BC、CA、AB的中点，点A2、B2、C2分别为△A1B1C1的边B1C1、C1A1、A1B1的中点，若△ABC的面积为1，则△A2B2C2的面积为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
由于A1、B1、C1分别是△ABC的边BC、CA、AB的中点，就可以得出△A1B1C1∽△ABC，且相似比为
，面积比为
，就可求出△A1B1C1的面积=，同样的方法得出△A2B2C2的面积=
．
解：∵A1、B1、C1分别是△ABC的边BC、CA、AB的中点，
∴A1B1、A1C1、B1C1是△ABC的中位线，
∴△A1B1C1∽△ABC，且相似比为，
∴S△A1B1C1：S△ABC=1：4，且S△ABC=1，
∴S△A1B1C1=．
∵A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点，
∴△A1B1C1∽△A2B2C2且相似比为，
∴△A2B2C2的面积=×S△A1B1C1=．
故选：D．
【题目】每年5月的第二个星期日即为母亲节，“父母恩深重，恩怜无歇时”，许多市民喜欢在母亲节为母亲送鲜花，感恩母亲，祝福母亲. 节日前夕，某花店采购了一批鲜花礼盒，成本价为30元每件，分析上一年母亲节的鲜花礼盒销售情况，得到了如下数据，同时发现每天的销售量
（件）是销售单价
（元/件）的一次函数.
销售单价 | … | 30 | 40 | 50 | 60 | … |
每天销售量 | … | 350 | 300 | 250 | 200 | … |
（1）求出与的函数关系；
（2）物价局要求,销售该鲜花礼盒获得的利润不得高于100﹪：
①当销售单价取何值时,该花店销售鲜花礼盒每天获得的利润为5000元?(利润=销售总价-成本价)；
②试确定销售单价取何值时，花店销该鲜花礼盒每天获得的利润
（元）最大？并求出花店销该鲜花礼盒每天获得的最大利润.
