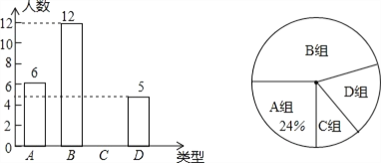
��Ŀ����
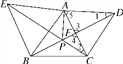
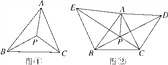
����Ŀ����ͼ����PΪ��ABC����ƽ����һ�㣬�ҡ�APB����BPC����CPA��120�������P������ABC�ķ����㣮
(1)�����PΪ��ǡ�ABC�ķ����㣬�ҡ�ABC��60��.
����֤�� ��ABP�ס�BCP��
����PA��3��PC��4����PB�ij���
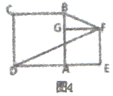
(2)��ͼ�ڣ���֪��ǡ�ABC���ֱ���AB��ACΪ������������ABE������ACD��CE��BD�ཻ�ڵ�P������AP.
�����CPD�Ķ�����
����֤����PΪ��ABC�ķ����㣮
���𰸡���1�������� ��2��60�� ��3��������
(1)��֤�����ߡ�PAB����PBA��180������APB��60������PBC����PBA����ABC��60�������PAB����PBC.�֡ߡ�APB����BPC��120�������ABP�ס�BCP
�ڽ⣺�ɢٿ�֪��ABP�ס�BCP���� ![]() ����PB2��PA��PC��12����PB��2
����PB2��PA��PC��12����PB��2![]() .
.
(2)�ٽ⣺��ͼ���ߡ�ABE�͡�ACD���������Σ���AE��AB��AC��AD����EAB����5��60��.�ߡ�EAC����EAB����BAC����BAD����BAC����5�����EAC����BAD�����ACE�ա�ADB�����1����2.�ߡ�3����4�����CPD����5��60��.
��֤�����ɢٿ�֪��1����2����3����4�����ADF�ס�PCF����AF��PF��DF��CF����AF��DF��PF��CF.�ߡ�AFP����CFD�����AFP�ס�DFC�����APF����ACD��60��.�ɢٿ�֪��CPD��60�������APC����CPD����APF��120������BPC��180������CPD��120�������APB��360������BPC����APC��120�������PΪ��ABC�ķ����㣮

����������������� ![]() ���ɷ�����Ķ����֪��APB����BPC��120����Ȼ����֤����PAB����PBC����֤����ABP�ס�BCP ���ɢٿ�֪��ABP�ס�BCP���õ�
���ɷ�����Ķ����֪��APB����BPC��120����Ȼ����֤����PAB����PBC����֤����ABP�ס�BCP ���ɢٿ�֪��ABP�ס�BCP���õ�![]() ���������
���������![]() �ij�.
�ij�.![]() ��ͼ
��ͼ![]() ��ʾ��������֤����ACE�ա�ADB�����1����2���ɡ�3����4�ɵõ���CPD����5��60��.
��ʾ��������֤����ACE�ա�ADB�����1����2���ɡ�3����4�ɵõ���CPD����5��60��.
���ɡ�CPD��60��.��֤����BPC��180������CPD��120����Ȼ��֤����ADF�ס�PCF�������������ε����ʺ��ж�������֤����AFP�ס�DFC���ʴ˿ɵõ���APF����ACD��60����Ȼ�����á�APC����CPD����APF��120��������������á�APB��360������BPC����APC��120��,����˵��.
���������
(1)�١ߡ�PAB����PBA��180������APB��60������PBC����PBA����ABC��60����
���PAB����PBC.
�֡ߡ�APB����BPC��120����
���ɢٿ�֪��ABP�ס�BCP��
��![]()
��PB2��PA��PC��12��
![]()
(2)����ͼ���ߡ�ABE����ACD���������Σ�
��AE��AB��AC��AD����EAB����5��60��.
�ߡ�EAC����EAB����BAC����BAD����BAC����5��
���EAC����BAD��
���ACE�ա�ADB��
���1����2.
�ߡ�3����4��
���CPD����5��60��.
���ɢٿ�֪��1����2����3����4��
���ADF�ס�PCF��
��AF��PF��DF��CF��
��AF��DF��PF��CF.
�ߡ�AFP����CFD��
���AFP�ס�DFC��
���APF����ACD��60��.
�ɢٿ�֪��CPD��60����
���APC����CPD����APF��120����
��BPC��180������CPD��120����
���APB��360������BPC����APC��120����
���PΪ��ABC�ķ����㣮