题目内容
【题目】在同一直角坐标系内分别作出一次函数y=![]() x+1和y=2x﹣2的图象,则下面的说法:
x+1和y=2x﹣2的图象,则下面的说法:
①函数y=2x﹣2的图象与y轴的交点是(﹣2,0);
②方程组![]() 的解是
的解是![]() ;
;
③函数y=![]() x+1和y=2x﹣2的图象交点的坐标为(﹣2,2);
x+1和y=2x﹣2的图象交点的坐标为(﹣2,2);
④两直线与y轴所围成的三角形的面积为3.
其中正确的有___.(填序号)
【答案】②④.
【解析】①当x=0时,y=2,所以函数y=2x2的图象与y轴的交点是(0,2),故①不正确;
②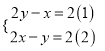 ,化简得:
,化简得: 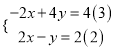 ,
,
(2)+(3)得:3y=6,y=2,∴x=2,
∴方程组{2yx=22xy=2的解是![]() ;故②正确;
;故②正确;
③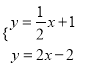 , 解得
, 解得![]() ,
,
∴函数y=![]() x+1和y=2x2的图象交点的坐标为(2,2);故③不正确;
x+1和y=2x2的图象交点的坐标为(2,2);故③不正确;
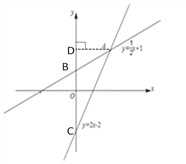
④如图所示,过A作AD⊥x轴于D,
当x=0时, 02=y, y= -2, 则C(0,-2),0 +1=y, y=1,则B(0,1),∴BC=3,
由③得A(2,2),则AD=2,∴ ![]() =
=![]() BCAD=
BCAD=![]() ×3×2=3,故④正确;
×3×2=3,故④正确;
故答案为:②④。

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目




