Question

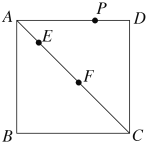
【题目】如图，在正方形中，、是对角线上的两个动点，是正方形四边上的任意一点，且，，设，当是等腰三角形时，下列关于点个数的说法中，一定正确的是（ ）

①当（即、两点重合）时，点有6个；

②当时，点最多有9个；

③当是等边三角形时，点有4个；

④当点有8个时，.

A.①③B.①④C.②④D.②③

Answer 1

【答案】A

【解析】

根据等腰三角形的性质，作图对各个说法进行分析判断，即可解决问题．

①如下图所示，

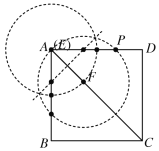
当x=0（即E、A两点重合）时，分别以E、F为圆心，EF的长为半径画圆，与正方形有4个交点，作EF的垂直平分线，与正方形有2个交点，所以P点有6个，

故①正确；
②当时，由图像可知P点最多有8个，如下图所示，

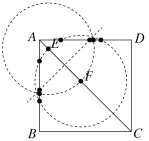
故②错误．
③如下图所示，

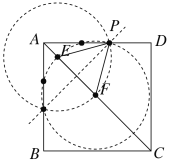
作法同①，当△PEF是等边三角形时，此时P点有4个，

故③正确；

④当P点有8个时，如下图所示：

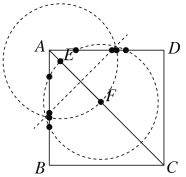
由①③图形以及对称性可知，当或或或时，P点有8个，故④错误；

综上，①③正确，
故选：A．