题目内容
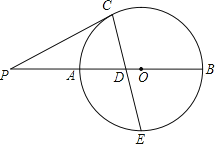
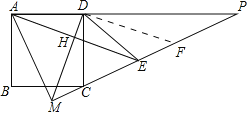
【题目】如图,正方形ABCD的边长为![]() ,E在正方形外,DE=DC,过D作DH⊥AE于H,直线DH,EC交于点M,直线CE交直线AD于点P,则下列结论正确的是____________
,E在正方形外,DE=DC,过D作DH⊥AE于H,直线DH,EC交于点M,直线CE交直线AD于点P,则下列结论正确的是____________

①∠DAE=∠DEA;②∠DMC=45°;③![]() ;④若MH=2,则S△CMD=
;④若MH=2,则S△CMD=![]()
【答案】①②③
【解析】
①利用等腰三角形的性质即可证明.
②根据DA=DC=DE,利用圆周角定理可知∠AEC=![]() ∠ADC=45°,即可解决问题.
∠ADC=45°,即可解决问题.
③如图,作DF⊥DM交PM于F,证明△ADM≌△CDF(SAS)即可解决问题.
④解直角三角形求出CE=EF=![]() 可得结论.
可得结论.
解:∵四边形ABCD是正方形,
∴DA=DC,∠ADC=90°,
∵DC=DE, ∴DA=DE, ∴∠DAE=∠DEA,故①正确,
∵DA=DC=DE,
![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上,
为半径的圆上,
∴∠AEC=![]() ∠ADC=45°(圆周角定理),
∠ADC=45°(圆周角定理),
∵DM⊥AE, ∴∠EHM=90°, ∴∠DMC=45°,故②正确,
如图,作DF⊥DM交PM于F,
∵∠ADC=∠MDF=90°,
∴∠ADM=∠CDF,
∵∠DMF=45°,
∴∠DMF=∠DFM=45°,
∴DM=DF,
∵DA=DC,
∴△ADM≌△CDF(SAS),
∴AM=CF,
∴AM+CM=CF+CM=MF=![]() DM,
DM,
∴ ![]() ,故③正确,
,故③正确,
![]()
![]()
![]() MH=2,
MH=2,
![]() AH=MH=HE=2,AM=EM=
AH=MH=HE=2,AM=EM=![]()
在Rt△ADH中,DH=![]()
∴DM=3,AM+CM=![]()
∴CM=CE=![]()
∴S△DCM=S△DCE,
故④错误.
故答案①②③.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目