��Ŀ����
��������ε�һ�����������ε�һ���ϣ�������������ֱ��������ε������������ϣ��������������ν��������ε��ڽ������Σ�
��1����ͼ�٣��ڡ�ABC�У�BC=a��BC���ϵĸ�AD=ha��EFGH�ǡ�ABC���ڽ������Σ���������EFGH�ı߳���x����֤��x=
��
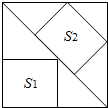
��2����Rt��ABC�У�AB=4��AC=3����BAC=90�ȣ�����ͼ�ڣ�ͼ���зֱ����ܵ��ڽ������Σ������ݼ���ش��ĸ��ڽ������ε�������
��3������ǡ�ABC�У�BC=a��AC=b��AB=c����a��b��c��������������ε��ڽ����������ĸ�������˵�����ɣ�

��1����ͼ�٣��ڡ�ABC�У�BC=a��BC���ϵĸ�AD=ha��EFGH�ǡ�ABC���ڽ������Σ���������EFGH�ı߳���x����֤��x=
| aha |
| a+ha |
��2����Rt��ABC�У�AB=4��AC=3����BAC=90�ȣ�����ͼ�ڣ�ͼ���зֱ����ܵ��ڽ������Σ������ݼ���ش��ĸ��ڽ������ε�������
��3������ǡ�ABC�У�BC=a��AC=b��AB=c����a��b��c��������������ε��ڽ����������ĸ�������˵�����ɣ�

��1����HG��BC��
���AHG����ABC��
��AM��AD=HG��BC��
�ࣨha-x����ha=x��a��
a��ha-x��=hax��
aha-ax=hax��
��a+ha��x=aha��
��x=
��
��2�����ݣ�1���Ľ������ͼ�ڵ������BC=
=5����AD=
��
��ʱ�����εı߳��ǣ�
=
��
��ͼ��ʱ�������εı߳���
=
��
�ʢ۵���������

��3�����ݣ�1���Ľ�����������ε������S����S=
aha����x=
��
�������ε�һ�����������ε����һ��BC��ʱ��a+ha��С����x����ڽ������ε�������
���AHG����ABC��
��AM��AD=HG��BC��
�ࣨha-x����ha=x��a��
a��ha-x��=hax��
aha-ax=hax��
��a+ha��x=aha��
��x=
| aha |
| a+ha |
��2�����ݣ�1���Ľ������ͼ�ڵ������BC=
| AB2+AC2 |
| 12 |
| 5 |
��ʱ�����εı߳��ǣ�
5��
| ||
5+
|
| 60 |
| 37 |
��ͼ��ʱ�������εı߳���
| 3��4 |
| 3+4 |
| 12 |
| 7 |
�ʢ۵���������

��3�����ݣ�1���Ľ�����������ε������S����S=
| 1 |
| 2 |
| S |
| 2(a+ha) |
�������ε�һ�����������ε����һ��BC��ʱ��a+ha��С����x����ڽ������ε�������

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ


 BD�ڵ�F��
BD�ڵ�F��


