Question

【题目】已知：如图，在正方形ABCD中，点E在边BC上，点F在边CD的延长线上，且BE=DF．

（1）求∠AEF的度数；

（2）如果∠AEB=75°，AB=2，求△FEC的面积．

Answer 1

【答案】（1）45°；（2）

【解析】（1）根据正方形的性质得到∠B=∠ADF=90°，AD=AB，求出∠ADF，根据SAS即可推出答案，再利用全等三角形的性质解答即可；（2）设EC=x．利用勾股定理计算即可．

解：（1）由正方形ABCD，得 AB=AD，∠B=∠ADF=∠BAD=90°，

在△ABE和△ADF中，

，

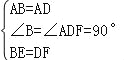∴△ABE≌△ADF，

∴∠BAE=∠FAD，AE=AF．

∴∠BAD=∠BAE+∠EAD=∠FAD+∠EAD=90°．

即得∠EAF=90°，

又∵AE=AF，

∴∠AEF=∠AFE=45°．

（2）∵∠AEB=75°，∠AEF=45°，

∴∠BEF=120°．

即得∠FEC=60°，

由正方形ABCD，得∠C=90°．∴∠EFC=30°．

∴EF=2EC，

设EC=x．则 EF=2x，BE=DF=2﹣x，CF=4﹣x．

在Rt△CEF中，由勾股定理，得 CE2+CF2=EF2．

即得 x2+（4﹣x）2=4x2．

解得，，（不合题意，舍去）．

∴，．

∴△FEC的面积为．