题目内容
【题目】教学实验:画∠AOB的平分线OC.
(1)将一块最够大的三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边分别于OA,OB交于E,F(如图①).度量PE、PF的长度,PEPF(填>,<,=); 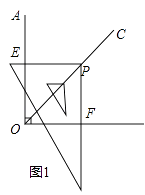
(2)将三角尺绕点P旋转(如图②): ①PE与PF相等吗?若相等请进行证明,若不相等请说明理由;
②若OP= ![]() ,请直接写出四边形OEPF的面积: .
,请直接写出四边形OEPF的面积: . 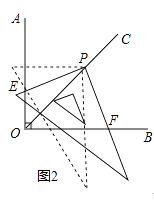
【答案】
(1)=
(2)1
【解析】(1)解:PE=PF; 所以答案是:=;(2)解:①PE=PF;理由如下:
把三角尺绕点P顺时针旋转,使三角尺的两条直角边分别与OA,OB垂直于M、N,如图所示:
则∠PME=∠PNF=90°,四边形OMPN是矩形
∵OP平分∠AOB,
∴PM=PN,
∴四边形OMPN是正方形,
∵∠AOB=∠PME=∠PNF=90°,
∴∠MPN=90°,
∵∠EPF=90°,
∴∠MPE=∠FPN,
在△PEM和△PFN中 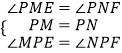
∴△PEM≌△PFN(ASA),
∴PE=PF.
②由①得:四边形OMPN是正方形,△PEM≌△PFN,
∴OM=ON= ![]() OP=1,四边形OEPF的面积=正方形OMPN的面积=OM2=1;
OP=1,四边形OEPF的面积=正方形OMPN的面积=OM2=1;
所以答案是:1.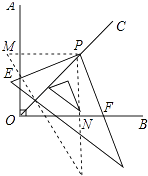

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目