题目内容
【题目】如图,菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.若EB=2,DF=3,∠EAF=60°,则△AEF的面积等于 . 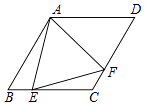
【答案】![]()
【解析】证明:如图,连接AC, 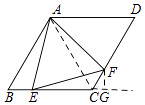
∵在菱形ABCD中,∠D=60°,AD=DC,
∴△ADC是等边三角形,
∵AC是菱形的对角线,
∴∠ACB= ![]() ∠DCB=60°,
∠DCB=60°,
∵∠FAC+∠EAC=∠FAC+∠DAF=60°,
∴∠EAC=∠DAF,
在△ADF和△ACE中,
∵ 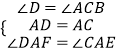 ,
,
∴△ADF≌△ACE(ASA),
∴DF=CE=3,AE=AF,BC=BE+CE=AB=5.
∴S四边形AECF=S△ACD
= ![]() ×5×5×sin60°
×5×5×sin60°
= ![]() ,
,
如图,过F作FG⊥BC于G,则
S△ECF= ![]() CECFsin∠GCF
CECFsin∠GCF
= ![]() CECFsin60°
CECFsin60°
= ![]() 6
6 ![]()
= ![]() ,
,
∴S△AEF=S四边形AECF﹣S△ECF
= ![]() ﹣
﹣ ![]()
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】利用菱形的性质和解直角三角形对题目进行判断即可得到答案,需要熟知菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目