题目内容
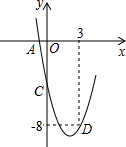
如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)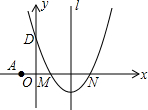 两点,且与y轴交于D(0,3),直线l是抛物线的对称轴.
两点,且与y轴交于D(0,3),直线l是抛物线的对称轴.
(1)求该抛物线的解析式.
(2)若过点A(-1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,求此直线的解析式.
(3)点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,求点P的坐标.
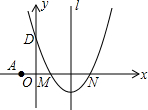 两点,且与y轴交于D(0,3),直线l是抛物线的对称轴.
两点,且与y轴交于D(0,3),直线l是抛物线的对称轴.(1)求该抛物线的解析式.
(2)若过点A(-1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,求此直线的解析式.
(3)点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,求点P的坐标.
(1)∵抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),
∴假设二次函数解析式为:y=a(x-1)(x-3),
将D(0,3),代入y=a(x-1)(x-3),
得:3=3a,∴a=1,
∴抛物线的解析式为:y=a(x-1)(x-3)=x2-4x+3;
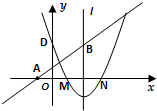
(2)∵过点A(-1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,
∴
AC×BC=6,
∵抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,
∴二次函数对称轴为x=2,
∴AC=3,
∴BC=4,
∴B点坐标为:(2,4)或(2,-4),
一次函数解析式为;y=kx+b,当点B为(2,4)时,
∴
,
解得:
,
∴y=
x+
;
当点B为(2,-4)时,
,
解得
,
∴y=-
x-
,
∴直线AB的解析式为:y=
x+
或y=-
x-
;
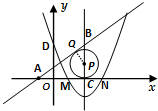
(3)∵当点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,
设⊙P与AB相切于点Q,与x轴相切于点C;
∴PQ⊥AB,AQ=AC,PQ=PC,
∵AC=1+2=3,BC=4,
∴AB=5,AQ=3,
∴BQ=2,
∵∠QBP=∠ABC,
∠BQP=∠ACB,
∴△ABC∽△PBQ,
∴
=
=
,
∴
=
,
∴PC=1.5,
P点坐标为:(2,1.5),
同理可得(2,-1•5),(2,-6),(2,6).
∴假设二次函数解析式为:y=a(x-1)(x-3),
将D(0,3),代入y=a(x-1)(x-3),
得:3=3a,∴a=1,
∴抛物线的解析式为:y=a(x-1)(x-3)=x2-4x+3;
(2)∵过点A(-1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,
∴
| 1 |
| 2 |
∵抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,
∴二次函数对称轴为x=2,
∴AC=3,
∴BC=4,
∴B点坐标为:(2,4)或(2,-4),
一次函数解析式为;y=kx+b,当点B为(2,4)时,
∴
|
解得:
|
∴y=
| 4 |
| 3 |
| 4 |
| 3 |
当点B为(2,-4)时,
|
解得
|
∴y=-
| 4 |
| 3 |
| 4 |
| 3 |
∴直线AB的解析式为:y=
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
(3)∵当点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,
设⊙P与AB相切于点Q,与x轴相切于点C;
∴PQ⊥AB,AQ=AC,PQ=PC,
∵AC=1+2=3,BC=4,
∴AB=5,AQ=3,
∴BQ=2,
∵∠QBP=∠ABC,
∠BQP=∠ACB,
∴△ABC∽△PBQ,
∴
| BQ |
| BC |
| PQ |
| AC |
| PC |
| AC |
∴
| 2 |
| 4 |
| PC |
| 3 |
∴PC=1.5,
P点坐标为:(2,1.5),
同理可得(2,-1•5),(2,-6),(2,6).



练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 于点C.
于点C.
 60度.
60度. 一次函数
一次函数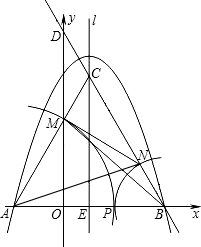 接AN、BM、MN.
接AN、BM、MN. 围起,栽上蝴蝶花,共用篱笆x0n,
围起,栽上蝴蝶花,共用篱笆x0n,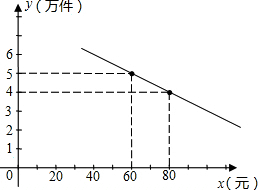 你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?