Question

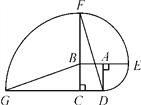
【题目】如图，四边形ABCD是边长为1的正方形，其中，，的圆心依次是点A，B，C.

(1)求点D沿三条圆弧运动到点G所经过的路线长；

(2)判断直线GB与DF的位置关系，并说明理由．

Answer 1

【答案】（1）3π（2）BG⊥DF

【解析】试题分析：(1)、扇形ADE的半径AD＝1，扇形BEF的半径BE＝BA＋AE＝BA＋AD＝2，扇形CFG的半径CF＝BC＋BF＝3，然后根据弧长的计算公式得出答案；(2)、首先得出△FCD和△GCB全等，然后根据全等的性质得出答案．

试题解析：(1)、．

(2)、∵CD=CB，CF=CG，∠FCD=∠GCB=90°， ∴△FCD≌△GCB， ∴∠BGC=∠CFD，

延长GB交FD于点H，∵∠GBC=∠FBH， ∠GBC+∠BGC=90°，∴∠FBH+∠CFD=90°，

∴∠BHF=90°，即BG⊥DF．