题目内容
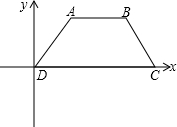
如图，在梯形ABCD中，DC∥AB，∠A+∠B=90°．若AB=10，AD=4，DC=5，
求梯形ABCD的面积．
求梯形ABCD的面积．
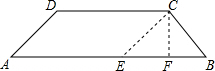
过C作CE∥AD交AB于E，过C作CF⊥AB于F．
∵DC∥AB，
∴四边形ADCE是平行四边形，
∴CE=AD=4AE=CD=5，∠CEB=∠A．
∵∠A+∠B=90°
∴∠ECB=90°
∴CB=
=
=3．
∵
CF•BE=
CE•CB，
∴CF=
∴S梯形ABCD=
（CD+AB）•CF=
（5+10）×
=18．
∵DC∥AB，
∴四边形ADCE是平行四边形，
∴CE=AD=4AE=CD=5，∠CEB=∠A．
∵∠A+∠B=90°
∴∠ECB=90°
∴CB=
| BE2-CE2 |
| 52-42 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CF=
| 12 |
| 5 |
∴S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| 5 |
练习册系列答案
阅读快车系列答案
相关题目
