题目内容
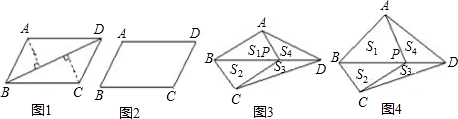
 已知,四边形ABCD中,∠ABC=∠ADB=90°,CE⊥BD于E,AB=5,AD=3,BC=
已知,四边形ABCD中,∠ABC=∠ADB=90°,CE⊥BD于E,AB=5,AD=3,BC= ,求四边形ABCD的面积S四边形ABCD.
,求四边形ABCD的面积S四边形ABCD.
解:在Rt△ABD中,AB=5,AD=3,
∴BD=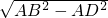 =
=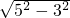 =4,
=4,
∵∠ABD+∠CBD=∠BCE+∠CBD=90°,
∴∠ABD=∠BCE,
∴cos∠ABD=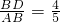 =cos∠BCE=
=cos∠BCE=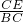 =
= ,
,
解得:CE= ,
,
∴S四边形ABCD=S△ABD+S△BCD= AD×BD
AD×BD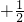 BD×CE=
BD×CE=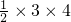
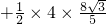 =6
=6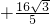 .
.
分析:要求四边形ABCD的面积只需求出三角形ABD和三角形BCD的面积,故只需求出BD和CE的长即可.
点评:本题考查了勾股定理的知识,难度适中,求出CE的长是解答本题的关键.
∴BD=
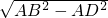 =
=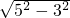 =4,
=4,∵∠ABD+∠CBD=∠BCE+∠CBD=90°,
∴∠ABD=∠BCE,
∴cos∠ABD=
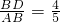 =cos∠BCE=
=cos∠BCE=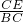 =
= ,
,解得:CE=
 ,
,∴S四边形ABCD=S△ABD+S△BCD=
 AD×BD
AD×BD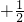 BD×CE=
BD×CE=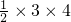
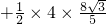 =6
=6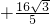 .
.分析:要求四边形ABCD的面积只需求出三角形ABD和三角形BCD的面积,故只需求出BD和CE的长即可.
点评:本题考查了勾股定理的知识,难度适中,求出CE的长是解答本题的关键.

练习册系列答案
相关题目
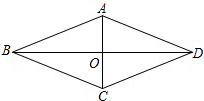 如图,已知,四边形ABCD是菱形,AC=6,BD=8,求AB的长和菱形ABCD的面积.
如图,已知,四边形ABCD是菱形,AC=6,BD=8,求AB的长和菱形ABCD的面积.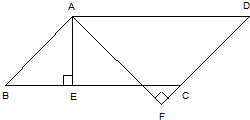 34、如图:在平行四边形ABCD中,∠B=30°,AE⊥BC于点E,AF⊥DC的延长线于点F,已知平行四边形ABCD的周长为40cm,且AE:AF=2:3.求平行四边形ABCD的面积.
34、如图:在平行四边形ABCD中,∠B=30°,AE⊥BC于点E,AF⊥DC的延长线于点F,已知平行四边形ABCD的周长为40cm,且AE:AF=2:3.求平行四边形ABCD的面积.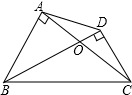 如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.
如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD. 如图,已知平行四边形ABCD,E是边AB的中点,联结AC、DE交于点O.记向量
如图,已知平行四边形ABCD,E是边AB的中点,联结AC、DE交于点O.记向量