题目内容
如图,抛物线的顶点坐标是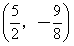 ,且经过点A(8,14)。
,且经过点A(8,14)。
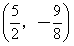 ,且经过点A(8,14)。
,且经过点A(8,14)。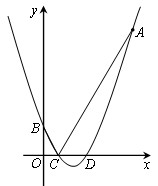
(1)求该抛物线的解析式;
(2)设该抛物线与y轴相交于点B,与x轴相交于C、D两点(点C在点D的左边),试求点B、C、D的坐标;
(3)设点P是x轴上的任意一点,分别连结AC、BC,试判断:PA+PB与AC+BC的大小关系,并说明理由。
(2)设该抛物线与y轴相交于点B,与x轴相交于C、D两点(点C在点D的左边),试求点B、C、D的坐标;
(3)设点P是x轴上的任意一点,分别连结AC、BC,试判断:PA+PB与AC+BC的大小关系,并说明理由。
解:(1)设抛物线的解析式为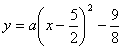
∵抛物线经过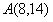
∴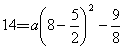
解得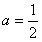
∴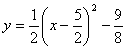 。
。
(2)令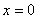 得
得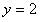
∴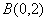
令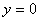 得
得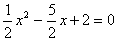
解得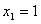 ,
,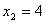
∴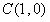 ,
,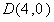 。
。
(3)结论: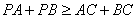
理由是:①当点P与点C重合时,有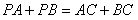
②当点P异于点C时,
∵直线AC经过点A(8,14)、C(1,0),
∴直线AC的解析式为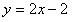
设直线AC与y轴相交于点E
令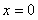 ,得
,得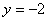
∴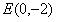
则点E(0,-2)与B(0,2)关于x轴对称
∴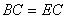
连接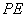
则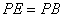
∴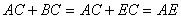
∵在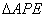 中,有
中,有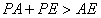
∴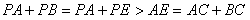
综上所得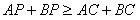 。
。
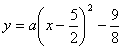
∵抛物线经过
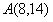
∴
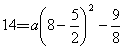
解得
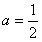
∴
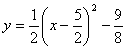 。
。(2)令
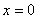 得
得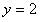
∴
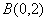
令
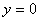 得
得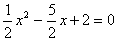
解得
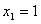 ,
,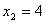
∴
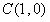 ,
,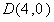 。
。(3)结论:
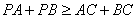
理由是:①当点P与点C重合时,有
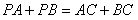
②当点P异于点C时,
∵直线AC经过点A(8,14)、C(1,0),
∴直线AC的解析式为
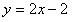
设直线AC与y轴相交于点E
令
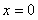 ,得
,得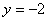
∴
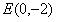
则点E(0,-2)与B(0,2)关于x轴对称
∴
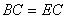
连接
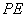
则
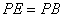
∴
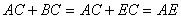
∵在
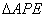 中,有
中,有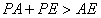
∴
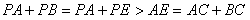
综上所得
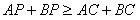 。
。
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
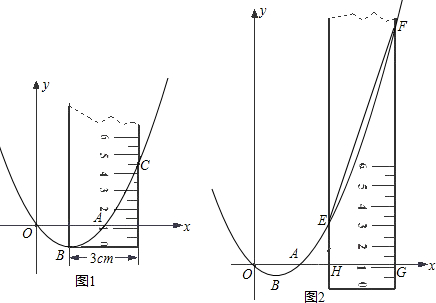
 在平面直角坐标系中,将一块腰长为
在平面直角坐标系中,将一块腰长为 在平面直角坐标系中,将一块腰长为
在平面直角坐标系中,将一块腰长为 cm的等腰直角三角板ABC如图放置,BC边与x轴重合,∠ACB=90°,直角顶点C的坐标为(-3,0).
cm的等腰直角三角板ABC如图放置,BC边与x轴重合,∠ACB=90°,直角顶点C的坐标为(-3,0).
