题目内容
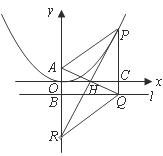
如图,在直角坐标系![]() 中,点
中,点![]() 为函数
为函数![]() 在第一象限内的图象上的任一点,点
在第一象限内的图象上的任一点,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 过
过![]() 且与
且与![]() 轴平行,过
轴平行,过![]() 作
作![]() 轴的平行线分别交
轴的平行线分别交![]() 轴,
轴,![]() 于
于![]() ,连结
,连结![]() 交
交![]() 轴于
轴于![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() .
.
(1)求证:![]() 点为线段
点为线段![]() 的中点;
的中点;
(2)求证:①四边形![]() 为平行四边形;②平行四边形
为平行四边形;②平行四边形![]() 为菱形;
为菱形;
(3)除![]() 点外,直线
点外,直线![]() 与抛物线
与抛物线![]() 有无其它公共点?并说明理由.
有无其它公共点?并说明理由.
证明:(1)法一:由题可知![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]() ,即
,即![]() 为
为![]() 的中点.
的中点.
法二:![]() ,
,![]() ,
,![]() .
.
又![]() 轴,
轴,![]() .
.
(2)①由(1)可知![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
又![]() ,
,![]() 四边形
四边形![]() 为平行四边形.
为平行四边形.
②设![]() ,
,![]() 轴,则
轴,则![]() ,则
,则![]() .
.
过![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,在
,在![]() 中,
中,
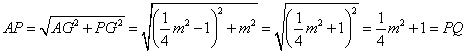 .
.
![]() 平行四边形
平行四边形![]() 为菱形.
为菱形.
(3)设直线![]() 为
为![]() ,由
,由![]() ,得
,得![]() ,
,![]() 代入得:
代入得:
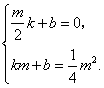
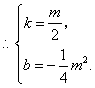
![]() 直线
直线![]() 为
为![]() .
.
设直线![]() 与抛物线的公共点为
与抛物线的公共点为![]() ,代入直线
,代入直线![]() 关系式得:
关系式得:
![]() ,
,![]() ,解得
,解得![]() .得公共点为
.得公共点为![]() .
.
所以直线![]() 与抛物线
与抛物线![]() 只有一个公共点
只有一个公共点![]() .
.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: