题目内容
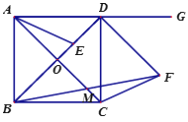
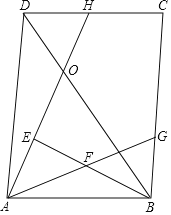
【题目】如图,在平行四边形ABCD中,点H为DC上一点,BD、AH交于点O,△ABO为等边三角形,点E在线段AO上,OD=OE,连接BE,点F为BE的中点,连接AF并延长交BC于点G,且∠GAD=60°.
(1)若CH=2,AB=4,求BC的长;
(2)求证:BD=AB+AE.
【答案】(1)![]() ;(2)详见解析
;(2)详见解析
【解析】
(1)延长AH、BC相交于点M,可证明△MCH∽△MBA,得出MH=AH,BM=2BC;由∠DOH=∠AOB=60°,∠ODH=∠OBA=60°,∠OHD=∠OAB=60°,可得△DOH是等边三角形,AE=OA-OE=OA-OD=2,得点E是OA的中点,根据“三线合一”可得BE的长度、BE⊥OA,根据勾股定理求出BM的长,而BC=![]() BM;
BM;
(2)AB=OB,由(1)知,AE=OE=OD,可证BD=OB+OD=AB+AE.
解:延长AH、BC相交于点M,
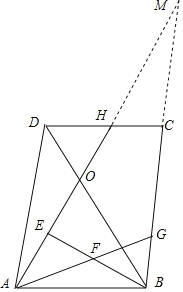
∵ABCD
∴CD=AB=4,CD∥AB
∴∠MHC=∠MAB,∠MCH=∠MBA
∴△MCH∽△MBA
![]()
∵CH=2
![]()
∴MH=AH,BM=2BC
∵△ABO为等边三角形
∴∠AOB=∠OAB=∠OBA=60°,OA=AB=4
∴∠DOH=∠AOB=60°
∴∠ODH=∠OBA=60°,∠OHD=∠OAB=60°
∴∠DOH=∠ODH=∠OHD
∴△DOH是等边三角形
∴OH=OD=DH=2
∴MH=AH=OA+OH=4+2=6,EM=OE+OH+MH=10
∵OD=OE=2
∴AE=OA﹣OE=4﹣2=2
∴点E是OA的中点
∵△ABO为等边三角形
∴BE⊥OA,∠ABE=30°
![]()
在Rt△BEM中,∠BEM=90°
∴BE2+EM2=BM2
![]()
![]()
![]()
(2)∵△ABO为等边三角形
∴AB=OB
由(1)知,AE=OE=OD
∵BD=OB+OD
∴BD=AB+AE