题目内容
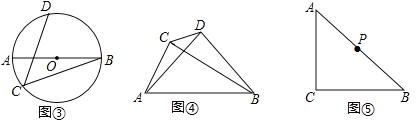
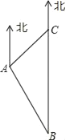
【题目】如图所示,在Rt△ABC中,∠ABC=90°,BF为斜边上的高,在射线AB上有点D,连接DF,作∠DFE=90°,FE交射线BC于点E.
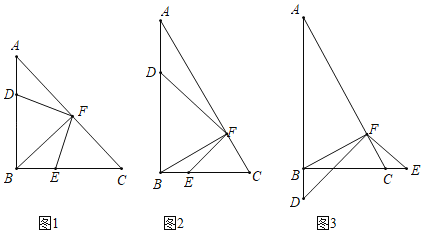
(问题发现)如图1所示,如果AB=CB,则DF与EF的数量关系为DF EF(选填>,<,=)
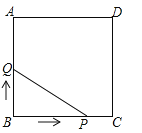
(类比探究)如图2所示,如果改变Rt△ABC中两直角边的比例,使得AB=2BC,则DF与EF还存在①中的关系吗?
(拓展延伸)如图3所示,在Rt△ABC中,如果已知BC=![]() ,AB=3,EF=
,AB=3,EF=![]() ,试求BD的长.
,试求BD的长.
【答案】【问题发现】:=;【类比探究】:不存在①中的关系,关系为:DF=2EF;【拓展延伸】:BD=![]() .
.
【解析】
问题发现:如图1,证明△ADF≌△BEF(SAS),得DF=EF;
类比探究:如图2所示,证明△ADF∽△BEF,得![]() ,则
,则![]() ,可得结论;
,可得结论;
拓展延伸:如图3,连接DE,设CE=a,根据勾股定理列等式:![]() ,解方程可得结论.
,解方程可得结论.
解:问题发现:
DF与EF的数量关系为DF=EF,理由是:
如图1,∵∠ABC=90°,AB=CB,
∴△ABC是等腰直角三角形,
∵BF⊥AC,
∴AF=CF=BF,∠ABF=∠CBF=45°,
∵∠AFD+∠BFD=∠BFD+∠BFE=90°,
∴∠AFD=∠BFE,
在△ADF和△BEF中,
∵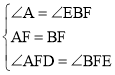 ,
,
∴△ADF≌△BEF(SAS),
∴DF=EF,
类比探究:
不存在①中的关系,关系为:DF=2EF,
理由是:如图2所示,∵∠A+∠ABF=∠A+∠C=90°,
∴∠ABF=∠C,
∵∠A=∠A,
∴△ABC∽△AFB,
∴![]() ,
,
∴![]() ,
,
∵∠A+∠ABF=∠ABF+∠CBF=90°,
∴∠A=∠CBF,
∵∠AFD+∠BFD=∠BFD+∠BFE=90°,
∴∠AFD=∠BFE,
在△ADF和△BEF中,
∵![]() ,
,
∴△ADF∽△BEF,
∴![]() ,
,
∵![]() ,AB=2BC,
,AB=2BC,
∴![]() ,
,
∴DF=2EF;
拓展延伸:
连接DE,设CE=a,
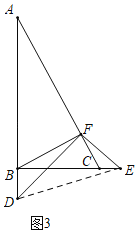
由以上结论可知: ![]() ,
,
∵EF=![]() ,CE=a,
,CE=a,
∴BD=![]() ,DF=
,DF=![]() ,
,
在Rt△DBE中,∠DBE=90°,得BD2+BE2=DE2,
在Rt△DFE中,∠DFE=90°,得DF2+EF2=DE2,
∴BD2+BE2=DF2+EF2,
即![]() ,
,
整理得:![]() ,
,
解得:a1=![]() ,a2=
,a2=![]() (舍),
(舍),
∴BD=![]() .
.