题目内容
【题目】如图,将△ABC绕顶点A顺时针旋转60°后得到△AB′C′,且C′为BC的中点.若D为B′C′与AB的交点,则C′D:DB′= .
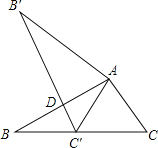
【答案】1:3.
【解析】
试题分析:旋转60°后,AC=AC′,旋转角∠C′AC=60°,可证△ACC′为等边三角形;再根据BC′=CC′=AC,证明△BC′D为30°的直角三角形,寻找线段C′D与DB′之间的数量关系.
解:根据旋转的性质可知:AC=AC′,∠AC′B′=∠C=60°,
∵旋转角是60°,即∠C′AC=60°,
∴△ACC′为等边三角形,
∴BC′=CC′=AC,
∴∠B=∠C′AB=30°,
∴∠BDC′=∠C′AB+∠AC′B′=90°,
即B′C′⊥AB,
∴BC′=2C′D,
∴BC=B′C′=4C′D,
∴C′D:DB′=1:3,
故答案为1:3.

练习册系列答案
相关题目

