题目内容
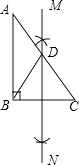
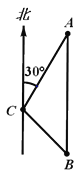
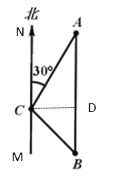
【题目】如图,一艘轮船位于灯塔C的北偏东30°方向上的A处,且A处距离灯塔C处80海里,轮船沿正南方向匀速航行一段时间后,到达位于灯塔C的东南方向上的B处.
(1)求灯塔C到达航线AB的距离;
(2)若轮船的速度为20海里/时,求轮船从A处到B处所用的时间(结果保留根号).
【答案】(1)40海里;(2)![]() 小时.
小时.
【解析】
(1)过点C作CD⊥AB,然后根据含30°的直角三角形性质 ;
(2)根据勾股定理求AB得长度,然后利用时间=路程÷速度公式求解.
解:(1)过点C作CD⊥AB,
由题意可知CN∥AB,∠NCA=30°
∴∠CAB=30°
∴在Rt△ACD中,![]()
答:点C到AB的距离为40海里;
(2)由题意可得:∠MCB=45°
∴在Rt△CDB中,∠DCB=45°
∴DB=CD=40
在Rt△ACD中,![]()
∴AB=AD+DB=![]()
∴轮船从A处到B处所用的时间为![]() (小时).
(小时).

练习册系列答案
相关题目