题目内容
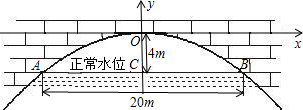
二次函数y=ax2+bx+c的图象如图所示．Q（n，2）是图象上的一点，且AQ⊥BQ．则a的值为______．
设ax2+bx+c=0的两根分别为x1与x2．
∴x1+x2=-
，x1x2=
，
∵AQ⊥BQ，
∴AQ2+BQ2=AB2．
∴（x1-n）2+4+（x2-n）2+4=（x1-x2）2，
化简得：n2-n（x1+x2）+4+x1x2=0．
∴n2+
n+4+
=0，
∴an2+bn+c=-4a．
∵（n，2）是图象上的一点，
∴an2+bn+c=2，
∴-4a=2，
∴a=-
．
故答案为：-
．
∴x1+x2=-
| b |
| a |
| c |
| a |
∵AQ⊥BQ，
∴AQ2+BQ2=AB2．
∴（x1-n）2+4+（x2-n）2+4=（x1-x2）2，
化简得：n2-n（x1+x2）+4+x1x2=0．
∴n2+
| b |
| a |
| c |
| a |
∴an2+bn+c=-4a．
∵（n，2）是图象上的一点，
∴an2+bn+c=2，
∴-4a=2，
∴a=-
| 1 |
| 2 |
故答案为：-
| 1 |
| 2 |
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
