Question

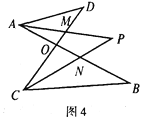
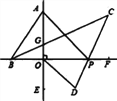
【题目】如图，直线AE⊥BF于O，将一个三角板ABO如图放置（∠BAO=30°），两直角边与直线BF，

AE重合，P为直线BF上一动点，BC平分∠ABP，PC平分∠APF，OD平分∠POE．

（1）求∠BGO的度数；

（2）试确定∠C与∠OAP之间的数量关系，并说明理由；

（3）P在直线上运动，∠C+∠D的值是否变化？若发生变化，说明理由；若不变求其值．

Answer 1

【答案】（1）60° ;（2）见解析； （3）∠C+∠D不变 ，理由见解析。

【解析】试题分析：（1）根据已知求出∠ABG的度数，运用外角的性质求出∠BGO的度数；

（2）根据外角的性质表示出∠C，得到∠C与∠OAP之间的数量关系；

（3）根据对顶角相等，分别表示出∠C和∠D，得到∠C+∠D的值．

试题解析：解：（1）∵∠BAO=30°，∴∠ABO=60°．∵BC平分∠ABP，∴∠ABG=∠GBO=30°，∠BGO=∠BAG+∠ABG=60°．

（2）∠C=∠OAP+15°．理由如下：

∠APF=∠OAP+∠AOP，∠C=∠APF﹣∠CBF=∠OAP+45°﹣30°=∠OAP+15°．

（3）∠C+∠D不变．理由如下：

∵∠CPF=∠OPD，∠CPF=∠C+30°，∠OPD=180°﹣45°﹣∠D，∴∠C+30°=180°﹣45°﹣∠D，∴∠C+∠D=105°．