题目内容
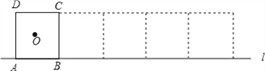
【题目】如图,将边长为1,中心为点O的正方形ABCD在直线l上按顺时针方向不滑动地每秒转动90°.
(1)第1秒点O经过的路线长为______,第2秒点O经过的路线长为______,第2013秒点O经过的路线长为______.
(2)分别求出第1秒、第2秒、第2013秒点A经过的路线长.
【答案】(1) ![]() π;
π; ![]() π;
π; ![]() π;(2)
π;(2) ![]() π;
π; ![]() π;
π; ![]() π;
π;
【解析】试题分析:(1)第1秒点O经过的路线长为以点B为圆心,OB长为半径,90°的圆弧;第2秒点O经过的路线长为以点C为圆心,OC长为半径,90°的圆弧,根据弧长公式计算即可,正方形每秒都要翻滚90°,翻转一周共四次,一共翻滚360°,算出OC的长等于![]() ,再求出正方形的中心O所经过的路径长;
,再求出正方形的中心O所经过的路径长;
(2)第1秒点A经过的路线长为以点B为圆心,AB长为半径,90°的圆弧,第2秒是C点为圆心CA为半径,第三秒D点为圆心DA为半径,第四秒A为圆心路径为0,4秒一个大周期,根据弧长公式计算即可.
试题解析:解:(1)∵AB=1,∴OC=![]() ,∴第1秒点O经过的路线长为
,∴第1秒点O经过的路线长为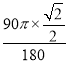 =
=![]() π,第2秒点O经过的路线长为
π,第2秒点O经过的路线长为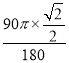 =
=![]() π,第2013秒点O经过的路线长为
π,第2013秒点O经过的路线长为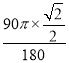 =
=![]() π,故答案为:
π,故答案为: ![]() π,
π, ![]() π,
π, ![]() π;
π;
(2)第1秒点A经过的路线长为![]() =
=![]() π,第2秒点A经过的路线长为
π,第2秒点A经过的路线长为![]() =
=![]() π,第2013秒点A经过的路线长为
π,第2013秒点A经过的路线长为![]() =
=![]() π.
π.

练习册系列答案
相关题目