题目内容
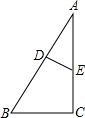已知：如图，D、E是△ABC的边AB、AC上的点，∠A=35°，∠C=85°，∠AED=60°．求证：AD•AB=AE•AC．
证明：在△ABC中，
∵∠A=35°，∠C=85°，
∴∠B=60°．
∵∠AED=60°且∠EAD=∠BAC，
∴△AED∽△ABC．
∴
．
∴AD•AB=AE•AC．
分析：把AD•AB=AE•AC变为比例式为，即证△AED∽△ABC，而这两个三角形现在共用一个∠A，且根据题意可知∠B=∠AED=60°，因此两三角形相似．
点评：此题主要考查了相似的判定与性质．题目比较简单，是相似三角形中的常规题目．
∵∠A=35°，∠C=85°，
∴∠B=60°．
∵∠AED=60°且∠EAD=∠BAC，
∴△AED∽△ABC．
∴
．∴AD•AB=AE•AC．
分析：把AD•AB=AE•AC变为比例式为
，即证△AED∽△ABC，而这两个三角形现在共用一个∠A，且根据题意可知∠B=∠AED=60°，因此两三角形相似．点评：此题主要考查了相似的判定与性质．题目比较简单，是相似三角形中的常规题目．
练习册系列答案
相关题目
交⊙O于F，GF切⊙O于F且与CP交于G，CH切⊙O于C且与AB的延长线交于H，如果GP2=GD•GC，AD平分∠BAP并交HP于M．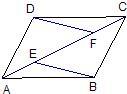
24、已知：如图，E、F是四边形ABCD的对角线AC上的两点，AF=CE，DF=BE，DF∥BE．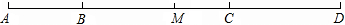
已知：如图正方形ABCD，E是BC的中点，F在AB上，且BF=
已知：如图，A、C是?DEBF的对角线EF所在直线上的两点，且AE=CF．