Question

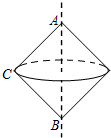如图，Rt△ABC中，∠ACB=90°，AC=BC=2

2

，若把Rt△ABC绕边AB所在直线旋转一周，则所得几何体的表面积为（　　）

• A、4π
• B、4

  2

  π
• C、8π
• D、8

  2

  π

Answer 1

分析：所得几何体的表面积为2个底面半径为2，母线长为2

2

的圆锥侧面积的和．

解答：解：∵Rt△ABC中，∠ACB=90°，AC=BC=2

2

，
∴AB=4，
∴所得圆锥底面半径为2，
∴几何体的表面积=2×π×2×2

2

=8

2

π，
故选D．

点评：考查有关圆锥的计算；得到所得几何体表面积的组成是解决本题的突破点；用到的知识点为：圆锥的侧面积=π×底面半径×母线长．