题目内容
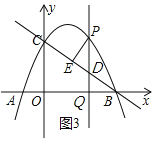
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C(0,2),
(1)求抛物线的函数表达式;
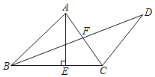
(2)如图,在抛物线对称轴上取两个点G、H(G在H的上方),且满足GH=1,连接CG,AH,求四边形CGHA的周长的最小值;
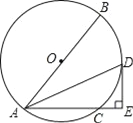
(3)如图,点P是抛物线第一象限的一个动点,过点P作PQ⊥x轴于点Q,交BC于点D,PE⊥BC于点E,设△PDE的面积为S,求当S取得最大值时点P的坐标,并求S的最大值.

【答案】(1)![]() (2)
(2)![]() +
+![]() +1.(3)点P的坐标为(2,3)时,S取最大值,最大值为
+1.(3)点P的坐标为(2,3)时,S取最大值,最大值为![]() .
.
【解析】
(1)由点A,B,C的坐标,利用待定系数法可求出抛物线的函数表达式;
(2)将抛物线的函数表达式变形为顶点式,可得出抛物线的对称轴,在y轴上截取CC′=GH(点C′在点C的下方),连接BC′交抛物线对称轴于点H,此时四边形CGHA的周长取最小值,由点C的坐标结合GH=1可得出点C′的坐标,由点A,C,B,C′的坐标利用勾股定理可求出AC,BC′的长度,将其代入四边形CGHA的周长的最小值=AC+BC′+GH中,即可求出结论;
(3)由点B,C的坐标,利用待定系数法可求出直线BC的函数表达式,设点P的坐标为(m,-![]() m2+
m2+![]() m+2)(0<m<4),则点D的坐标为(m,-
m+2)(0<m<4),则点D的坐标为(m,-![]() m+2),进而可得出PD的长度,由PE⊥BC,PQ⊥x轴及∠PDE=∠BDQ可得出∠DPE=∠DBQ,结合tan∠DPE=
m+2),进而可得出PD的长度,由PE⊥BC,PQ⊥x轴及∠PDE=∠BDQ可得出∠DPE=∠DBQ,结合tan∠DPE=![]() 可得出PE=2DE,PD=
可得出PE=2DE,PD=![]() DE,再利用三角形的面积公式可得出S=
DE,再利用三角形的面积公式可得出S=![]() PD2,由PD=-
PD2,由PD=-![]() m2+2m,利用二次函数的性质可求出PD的最大值,代入S=
m2+2m,利用二次函数的性质可求出PD的最大值,代入S=![]() PD2中即可求出S的最大值.
PD2中即可求出S的最大值.
(1)将A(-1,0),B(4,0),C(0,2)代入y=ax2+bx+c,得:
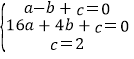 ,解得:
,解得: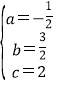 ,
,
∴抛物线的函数表达式为y=-![]() x2+
x2+![]() x+2.
x+2.
(2)∵y=-![]() x2+
x2+![]() x+2=-
x+2=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
∴抛物线的对称轴为直线x=![]() .
.
如图2,在y轴上截取CC′=GH(点C′在点C的下方),连接BC′交抛物线对称轴于点H.
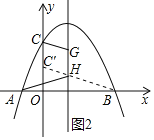
∵CC′∥GH,
∴四边形CC′HG为平行四边形,
∴C′H=CG.
又∵点A,B关于抛物线的对称轴对称,
∴BH=AH,
∴AH+CG=BH+C′H=BC′,即此时四边形CGHA的周长取最小值.
∵点C的坐标为(0,2),GH=1,
∴点C′的坐标为(0,1).
∵点A的坐标为(-1,0),点B的坐标为(4,0),
∴AC=![]() =
=![]() ,BC′=
,BC′=![]() =
=![]() ,
,
∴四边形CGHA的周长的最小值=AC+BC′+GH=![]() +
+![]() +1.
+1.
(3)设直线BC的函数表达式为y=kx+d(k≠0),
将B(4,0),C(0,2)代入y=kx+d,得:
![]() ,解得:
,解得: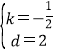 ,
,
∴直线BC的函数表达式为y=-![]() x+2.
x+2.
设点P的坐标为(m,-![]() m2+
m2+![]() m+2)(0<m<4),则点D的坐标为(m,-
m+2)(0<m<4),则点D的坐标为(m,-![]() m+2),
m+2),
∴PD=-![]() m2+
m2+![]() m+2-(-
m+2-(-![]() m+2)=-
m+2)=-![]() m2+2m.
m2+2m.
∵PE⊥BC,PQ⊥x轴,
∴∠PED=∠BQD=90°.
∵∠PDE=∠BDQ,
∴∠DPE=∠DBQ,
∴tan∠DPE=![]() ,
,
∴PE=2DE,PD=![]() DE,
DE,
∴S=![]() DEPE=
DEPE=![]() ×
×![]() PD×
PD×![]() PD=
PD=![]() PD2.
PD2.
∵在PD=-![]() m2+2m=-
m2+2m=-![]() (m-2)2+2中,-
(m-2)2+2中,-![]() <0,
<0,
∴当m=2时,PD取最大值,最大值为2,
∴当点P的坐标为(2,3)时,S取最大值,最大值为![]() .
.

 名校课堂系列答案
名校课堂系列答案