题目内容
【题目】如图,在四边形ABCD中, ∠B=90°,DE//AB交BC于E、交AC于F,∠CDE=∠ACB=30°,BC=DE.
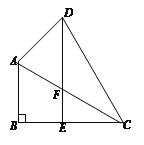
(1)求证:△ACD是等腰三角形;
(2)若AB=4,求CD的长.
【答案】(1)详见解析;(2)8.
【解析】
试题(1)先根据条件证明△ABC≌△CED就可以得出∠CDE=∠ACB=30°,再计算出∠DCF=30°,这样就可以得出结论;
(2)根据AB=4就可以求出AC的值,就可以求出CD.
试题解析:(1)∵DE∥AB,
∴∠DEC=∠B.
在△ABC和△CED中
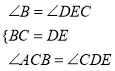 ,
,
∴△ABC≌△CED(ASA)
∴∠CDE=∠ACB=30°,
∴∠DCE=30°,
∴∠DCF=∠DCE-∠ACB=30°,
∴∠DCF=∠CDF,
∴△FCD是等腰三角形;
(2)∵∠B=90°,∠ACB=30°,
∴AC=2AB.
∵AB=4,
∴AC=8,
∴CD=8.
答:CD=8.

练习册系列答案
相关题目