题目内容
4、等腰△ABC的顶角A为120°,过底边上一点D作底边BC的垂线交AC于E,交BA的延长线于F,则△AEF是( )
分析:由AB=AC可以得到∠B=∠C,又∠AEF=∠DEC=90°-∠C,∠F=90°-∠B,可以推出∠AEF=∠F,又利用∠A=120°可以求出∠FAE=60°,最后可以证明△AEF是等边三角形.
解答: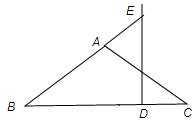 证明:如图,∵AB=AC,
证明:如图,∵AB=AC,
∴∠B=∠C.
∵∠AEF=∠DEC=90°-∠C,
∠F=90°-∠B,
∴∠AEF=∠F.
又∠A=120°,
∴∠FAE=60°.
∴△AEF是等边三角形.
故选A.
 证明:如图,∵AB=AC,
证明:如图,∵AB=AC,∴∠B=∠C.
∵∠AEF=∠DEC=90°-∠C,
∠F=90°-∠B,
∴∠AEF=∠F.
又∠A=120°,
∴∠FAE=60°.
∴△AEF是等边三角形.
故选A.
点评:此题主要考查了等边三角形的判定,综合利用了等腰三角形和直角三角形的性质.

练习册系列答案
相关题目
等腰△ABC的顶角∠A=135°,E、F是B、C上两点,且BF=BA,CE=CA,则∠EAF=( )度.
| A、15 | B、22.5 | C、35.5 | D、45 |
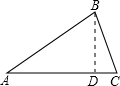 如图,等腰△ABC的顶角∠A=30°,腰长AB=2,BD为AC边上的高,根据已知条件,可求出tan15°的值为
如图,等腰△ABC的顶角∠A=30°,腰长AB=2,BD为AC边上的高,根据已知条件,可求出tan15°的值为 如图,等腰△ABC的顶角为120°腰长为8,则底边上的中线AD=
如图,等腰△ABC的顶角为120°腰长为8,则底边上的中线AD=