题目内容
等腰△ABC的顶角∠A=135°,E、F是B、C上两点,且BF=BA,CE=CA,则∠EAF=( )度.
| A、15 | B、22.5 | C、35.5 | D、45 |
分析:首先根据三角形内角和定理求出∠B+∠C的度数,进而可根据等腰三角形的性质表示出∠AEF+∠AFE的度数,从而根据三角形内角和定理求出∠EAF的度数.
解答:解:∵∠A=135°,
∴∠B+∠C=45°;
△BAF中,BA=BF,∠BFA=
(180°-∠B);
同理可求得,∠CEA=
(180°-∠C);
∴∠BFA+∠CEA=180°-
(∠B+∠C);
故∠EAF=
(∠B+∠C)=22.5°;
故选B.
∴∠B+∠C=45°;
△BAF中,BA=BF,∠BFA=
| 1 |
| 2 |
同理可求得,∠CEA=
| 1 |
| 2 |
∴∠BFA+∠CEA=180°-
| 1 |
| 2 |
故∠EAF=
| 1 |
| 2 |
故选B.
点评:此题主要考查等腰三角形的性质,以及三角形内角和定理.利用三角形内角和求解各角是一种比较重要的方法,注意掌握.

练习册系列答案
相关题目
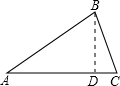 如图,等腰△ABC的顶角∠A=30°,腰长AB=2,BD为AC边上的高,根据已知条件,可求出tan15°的值为
如图,等腰△ABC的顶角∠A=30°,腰长AB=2,BD为AC边上的高,根据已知条件,可求出tan15°的值为 如图,等腰△ABC的顶角为120°腰长为8,则底边上的中线AD=
如图,等腰△ABC的顶角为120°腰长为8,则底边上的中线AD=