题目内容
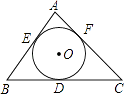
【题目】如图，在周长为12的菱形ABCD中，CE=1，CF=2，若点P为对角线BD上一动点，则PE+PF的最小值是（ ）
A. 
B. 2 C. 3 D. 5
【答案】C
【解析】
作F点关于BD的对称点F , 则PF=PF , 由两点之间线段最短可知当E、 P、 F 在一条直线上时,EP+FP有最小值, 然后求得EF 的长度即可.
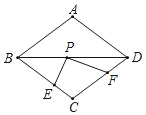
解：如图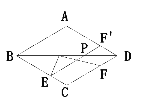
作F点关于BD的对称点F',则PF=PF',连接EF'交BD于点P.
EP+FP=EP+F'P.
由两点之间线段最短可知: 当E、P 、F'在一条直线上时,EP+FP的值最小,此时
EP+FP=EP+F'P=EF'.
四边形ABCD为菱形,周长为12,
AB=BC=CD=DA=3,AB //CD,
CF=2, CE=1,
D F'=DF=1,
四边形CEF'D是平行四边形,
EF'=CD=3.
EP+FP的最小值为3.
故选C.
练习册系列答案
阅读快车系列答案
相关题目
【题目】6月5日是世界环境日，某校组织了一次环保知识竞赛，每班选25名同学参加比赛，成绩分别为A、B、C、D四个等级，其中相应等级的得分依次记为100分、90分、80分、70分，学校将某年级的一班和二班的成绩整理并绘制成统计图： 根据以上提供的信息解答下列问题：
（1）把一班竞赛成绩统计图补充完整；
（2）写出下表中a、b、c的值：
平均数（分） | 中位数（分） | 众数（分） | |
一班 | a | b | 90 |
二班 | 87.6 | 80 | c |
（3）请从以下给出的三个方面中任选一个对这次竞赛成绩的结果进行分析： ①从平均数和中位数方面比较一班和二班的成绩；②从平均数和众数方面比较一班和二班的成绩；③从B级以上（包括B级）的人数方面来比较一班和二班的成绩．
