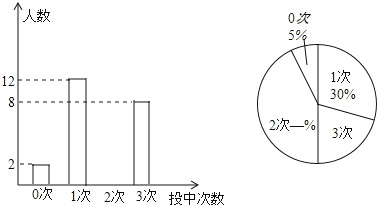
题目内容
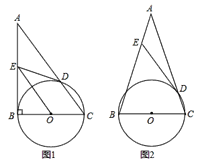
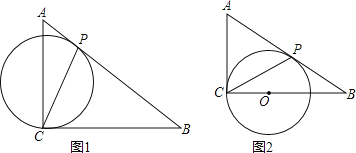
【题目】如图1,Rt△ACB中,AC=3,BC=4,有一动圆⊙O始终与Rt△ACB的斜边AB相切于动点P,且⊙O始终经过直角顶点C.
(1)如图2,当⊙O 运动至与直角边AC相切时,求此时⊙O 的半径r的长;
(2)试求⊙O 的半径r的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由勾股定理先求出AB的值,根据切线长定理得出AP=AC,求出BP的长,再利用△ACB∽△OPB对应边成比例得出圆的半径.
(2)先作出⊙O最大半径时的图,结合三角函数计算r的值.
(1)连接OP,
在Rt△ACB中,AC=3,BC=4,
∴AB=![]() =
=![]() =5,
=5,
∵AC,AP都是圆的切线,
∴AP=AC=3,
∴PB=2,
∵∠ACB=∠OPB=90°,∠B=∠B,
∴△ACB∽△OPB,
∴![]() ,
,
∴![]() ,
,
∴r=![]() .
.
(2)如图,当点P与点B重合时,⊙O的半径最大,此时点O在BC的垂直平分线上,
过点O作OD⊥BC于点D,则BD=![]() BC,
BC,
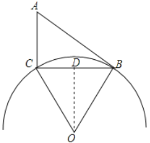
∵AB是切线,
∴∠ABO=90°,
∴∠ABC+∠OBD=∠BOD+∠OBD=90°,
∴∠ABC=∠BOD,
∴sin∠BOD= sin∠ABC=![]() =
=![]() =
=![]() ,
,
∴OB=![]() ,
,
即半径的最大值为![]() .
.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() , 纵坐标
, 纵坐标![]() 的对应值如下表:
的对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的是 .
①抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ; ②抛物线与
; ②抛物线与![]() 轴的交点为
轴的交点为![]() ;
;
③抛物线的对称轴是:直线![]() ; ④在对称轴左侧
; ④在对称轴左侧![]() 随
随![]() 增大而增大.
增大而增大.