题目内容
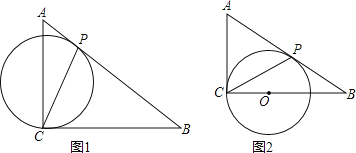
【题目】如图,以△ABC的边BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点E.
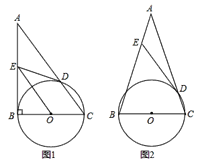
(1)如图1,若∠ABC=90°,求证:OE∥AC;
(2)如图2,已知AB=AC,若sin∠ADE=![]() , 求tanA的值.
, 求tanA的值.
【答案】(1)详见解析;(2)tan∠A=![]() .
.
【解析】
(1)连结OD,如图1,先根据切线的性质得到∠ODE=90°,然后通过HL证明Rt△OBE≌Rt△ODE,得到∠1=∠2,利用三角形的外角性质得到∠2=∠C,再根据平行线的判定定理即可得证;
(2)连结OD,作OF⊥CD于F,DH⊥OC于H,如图2,易证∠A=∠COD,根据切线的性质与两角互余可得∠ADE=∠DOF,则在Rt△DOF中,sin∠DOF=![]() =
=![]() ,设DF=x,则OD=3x,然后用含x的式子表示相关线段的长,然后求得tanA的值即可.
,设DF=x,则OD=3x,然后用含x的式子表示相关线段的长,然后求得tanA的值即可.
解:(1)证明:连结OD,如图1,
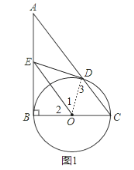
∵DE为⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,
在Rt△OBE和Rt△ODE中,
![]() ,
,
∴Rt△OBE≌Rt△ODE,
∴∠1=∠2,
∵OC=OD,
∴∠3=∠C,
而∠1+∠2=∠C+∠3,
∴∠2=∠C,
∴OE∥AC;
(2)解:连结OD,作OF⊥CD于F,DH⊥OC于H,如图2,
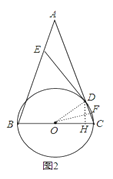
∵AB=AC,OC=OD,
而∠ACB=∠OCD,
∴∠A=∠COD,
∵DE为⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,
∴∠ADE+∠ODF=90°,
而∠DOF+∠ODF=90°,
∴∠ADE=∠DOF,
∴sin∠DOF=sin∠ADE=![]() ,
,
在Rt△DOF中,sin∠DOF=![]() =
=![]() ,
,
设DF=x,则OD=3x,
∴OF=![]() =2
=2![]() x,DF=CF=x,OC=3x,
x,DF=CF=x,OC=3x,
∵![]() DHOC=
DHOC=![]() OFCD,
OFCD,
∴DH=![]() =
=![]() x,
x,
在Rt△ODH中,OH=![]() =
=![]() x,
x,
∴tan∠DOH=![]() =
=![]() =
=,
∴tan∠A=![]() .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目