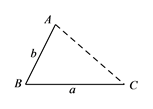题目内容
【题目】我国魏晋时期的数学家刘徽创立了“割圆术”，认为圆内接正多边形边数无限增加时，周长就越接近圆周长，由此求得了圆周率
的近似值．设半径为
的圆内接正
边形的周长为
，圆的直径为
．如右图所示，当
时，
，那么当
时，
．（结果精确到
，参考数据：
）
【答案】3.10.
【解析】
试题解析：如图，
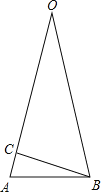
圆的内接正十二边形被半径分成如图所示的十二个等腰三角形，其顶角为30°，即∠O=30°，∠ABO=∠A=75°，
作BC⊥AO于点C，则∠ABC=15°，
∵AO=BO=r，
∴BC=
r，OC=
r，
∴AC=（1-）r，
∵Rt△ABC中，cosA=
，
即0.259=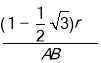
，
∴AB≈0.517r，
∴L=12×0.517r=6.207r，
又∵d=2r，
∴
≈3.10.
练习册系列答案
阅读快车系列答案
相关题目
