题目内容
点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数 的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是
的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是
| A.y3<y1<y2 | B.y1<y2<y3 | C.y3<y2<y1 | D.y2<y1<y3 |
A.
解析试题分析:先根据反比例函数的解析式判断出函数图象所在的象限,再根据x1<x2<0<x3即可得出结论.
∵反比例函数y=-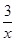 中k=-3<0,
中k=-3<0,
∴函数图象的两个分支分别位于二、四象限,且在每一象限内,y随x的增大而减小.
∵x1<x2<0,
∴A、B两点在第二象限,C点在第三象限,
∴y2>y1>y3.
故选A.
考点: 反比例函数图象上点的坐标特征.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
已知反比例函数y= 的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是( )
的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是( )
| A.(﹣6,1) | B.(1,6) | C.(2,﹣3) | D.(3,﹣2) |
在反比例函数 的图象的每一条曲线上,
的图象的每一条曲线上, 都随着
都随着 的增大而增大,则
的增大而增大,则 的值可以是( )
的值可以是( )
A. | B.0 | C.1 | D.2 |
已知 是反比例函数
是反比例函数 的图象上的三点,且
的图象上的三点,且 ,则
,则 的大小关系是 ( )
的大小关系是 ( )
A. | B. | C. | D. |
下列各点在反比例函数 的图象上的是( )
的图象上的是( )
| A.(-1,-2) | B.(-1,2) | C.(-2,-1) | D.(2,1) |
如图,A是反比例函数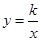 的图像上的一点,AB⊥x轴于点B,且△ABO的面积是3,则k的值是( )
的图像上的一点,AB⊥x轴于点B,且△ABO的面积是3,则k的值是( )
| A.3 | B.-3 | C.-6 | D.6 |
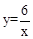 上,且OA=4,过A作AC⊥x轴,垂足为C, OA的垂直平分线交OC于B,则△ABC的周长为( )
上,且OA=4,过A作AC⊥x轴,垂足为C, OA的垂直平分线交OC于B,则△ABC的周长为( )




 与
与 成反比例,且当
成反比例,且当 时,
时, ,那么当
,那么当 时,
时, .
.