题目内容
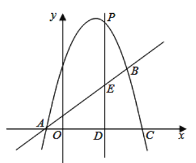
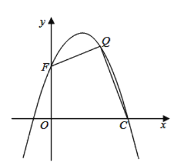
【题目】如图,反比例函数图象在第一象限的分支上有一点C(1,3),过点C的直线y = kx+b〔k< 0〕与x轴交于点A.
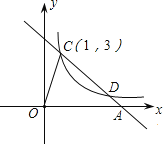
(1)求反比例函数的解析式;
(2)当直线与反比例函数的图象在第一象限内的另一交点的横坐标为3时,求△COD的面积.
【答案】(1)![]() ;(2)4.
;(2)4.
【解析】
(1)∵点C(1,3)在反比例函数图象上,∴k1=1×3=3可求反比例函数的解析式;
(2)由直线与反比例函数的图象在第一象限内的另一交点的横坐标为3,易求其解析式,进而求出直线与x轴交点坐标,即可求出△COD的面积.
(1)∵点C(1,3)在反比例函数图象上,
∴k=1×3=3,
∴y=![]() ;
;
(2)当x=3时,y=![]() =1,
=1,
∴D(3,1).
∵C(1,3)、D(3,1)在直线y=k2x+b上,
∴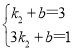 ,
,
∴![]() .
.
∴y=-x+4.
令y=0,则x=4,
∴A(4,0),
∴S△COA=![]() ×4×3=6,
×4×3=6,
S△DOA=![]() ×4×1=2,
×4×1=2,
∴△COD的面积=S△COA-S△DOA=6-2=4.

练习册系列答案
相关题目