题目内容
【题目】如图,AB∥CD,直L交AB、CD分别于点E、F,点M在线段EF上(点M不与E、F重合),N是直线CD上的一个动点(点N不与F重合)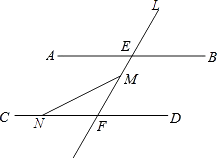
(1)当点N在射线FC上运动时(F点除外),则∠FMN+∠FNM=∠AEF,说明理由?
(2)当点N在射线FD上运动时(F点除外),∠FMN+∠FNM与∠AEF有什么关系?画出图形,猜想结论并证明.
【答案】
(1)
解:∵AB∥CD,
∴∠AEF+∠MFN=180°.
∵∠MFN+∠FMN+∠FNM=180°,
∴∠FMN+∠FNM=∠AEF.
(2)
解:∠FMN+∠FNM+∠AEF=180°.
理由:如图所示,
∵AB//CD,
∴∠AEF=∠MFN.
∵∠MFN+∠FMN+∠FNM=180°,
∴∠FMN+∠FNM+∠AEF=180°.
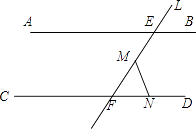
【解析】(1)利用两直线平行,同旁内角互补和三角形的内角和为180°,易得∠FMN+∠FNM=∠AEF;(2)根据两直线平行,内错角相等和三角形的内角和为180度,易得∠FMN+∠FNM+∠AEF=180°.
【考点精析】认真审题,首先需要了解平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为保证中小学生每天锻炼一小时,某校开展了形式多样的体育活动项目,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的频率统计表和频数分布直方图.请你根据图表信息完成下列各题:
(1)填空: a= ;m= ;n= ;
(2)请将条形统计图补充完整;
(3)该校共有学生1500人,估计参加乒乓球项目的学生有 人;
运动项目 | 频数(人数) | 频率 |
篮球 | 20 | 0.40 |
乒乓球 | n | 0.10 |
足球 | 10 | m |
其他 | 15 | 0.30 |
合计 | a | 1.00 |