题目内容
【题目】如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A与C重合,D与G重合.若长方形的长BC为8,宽AB为4,求: 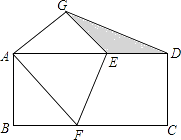
(1)CF的长;
(2)EF的长;
(3)求阴影部分三角形GED的面积.
【答案】
(1)解:设CF=x,则BF=8﹣x,
在Rt△ABF中,AB2+BF2=AF2,
∴16+(8﹣x)2=x2,
解得:x=5,
∴CF=5
(2)解:过F点作FH⊥AD于H,则
FH=4,EH=AE﹣AH=2,
∴EF2=42+22=20,
∴EF=2 ![]()
(3)解:过G点作GM⊥AD于M,则AG×GE=AE×GM,AG=AB=4,AE=CF=5,GE=DE=3,
∴GM= ![]() ,
,
∴S△GED= ![]() ×GM×DE=
×GM×DE= ![]() .
.

【解析】(1)设CF=x,则BF=8﹣x,在Rt△ABF中,AB2+BF2=AF2 , 解方程可求出CF的长;(2)过F点作FH⊥AD于H,在Rt△EHF中根据勾股定理可求出EF的长;(3)过G点作GM⊥AD于M,根据三角形面积不变性,AG×GE=AE×GM,求出GM的长,根据三角形面积公式计算即可.
【考点精析】通过灵活运用翻折变换(折叠问题),掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等即可以解答此题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目