题目内容
【题目】如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE=DF，连接BF、CE，且∠FBD=35°，∠BDF=75°，下列说法：①△BDF≌CDE；②ABD和△ACD面积相等；③BF∥CE；④∠DEC=70°，其中正确的有（ ）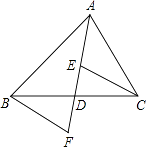 
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】解：∵AD是△ABC的中线， ∴BD=CD，
∴△ABD的面积=△ACD的面积，
在△BDF和△CDE中，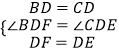 
，
∴△BDF≌△CDE（SAS），故①②正确
∴∠F=∠CED，∠DEC=∠F，
∴BF∥CE，故③正确，
∵∠FBD=35°，∠BDF=75°，
∴∠F=180°﹣35°﹣75°=70°，
∴∠DEC=70°，故④正确；
综上所述，正确的是①②③④4个．
故答案为：D．
根据三角形中线的定义可得BD=CD，得出△ABD的面积=△ACD的面积，然后利用“边角边”证明△BDF和△CDE全等，由全等三角形的性质得出∠F=∠CED，∠DEC=∠F，再根据内错角相等，两直线平行可得BF∥CE，最后根据三角形内角和定理求出∠F，得出④正确，即可得出结论．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】在一次实验中，小明把一根弹簧的上端固定，在其下端悬挂物体，下面是测得的弹簧的长度y与所挂物体的质量x的一组对应值：
所挂重量x（kg） | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧长度y（cm） | 18 | 20 | 22 | 24 | 26 | 28 |
（1）上述反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
（2）写出y与x之间的关系式，并求出当所挂重物为6kg时，弹簧的长度为多少？
