��Ŀ����
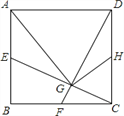
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=3��BC=4������B������BB1��AC������D�ӵ�A����������AC������ÿ��5����λ���ٶ��˶���ͬʱ����E�ӵ�C������AC������ÿ��3����λ���ٶ��˶�������D��DH��AB��H������E��EF��AC������BB1��F��G��EF�е㣬����DG�����D�˶���ʱ��Ϊt�룮
��1����tΪ��ֵʱ��AD=AB���������ʱDE�ij��ȣ�
��2������DEG���ACB����ʱ����t��ֵ��

���𰸡���1����t=1ʱ��AD=AB��AE=1��
��2����t=![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ʱ����DEG����ACB����.
ʱ����DEG����ACB����.
�������������������1�����ݹ��ɶ����ó�AB=5,ҪʹAD=AB=5��������Dÿ��5����λ���ٶ��˶�����t=1����2������DEG����ACB����ʱ��Ҫ������������ۣ��������������ε����ʣ��г�����ʽ�����DE�ı���ʽʱ��Ҫ��AD��AE��AD��AE�����������.
���������
��1���ߡ�ACB=90�㣬AC=3��BC=4�� ��AB=![]() =5��
=5��
��AD=5t��CE=3t�� ����AD=ABʱ��5t=5����t=1��
��AE=AC+CE=3+3t=6��DE=6��5=1��
��2����EF=BC=4��G��EF���е㣬 ��GE=2��
��AD��AE����t��![]() ��ʱ��DE=AE��AD=3+3t��5t=3��2t��
��ʱ��DE=AE��AD=3+3t��5t=3��2t��
����DEG����ACB���ƣ��� ![]() ��
�� ![]() ��
��
��![]() ��
��![]() �� ��t=
�� ��t=![]() ��t=
��t=![]() ��
��
��AD��AE����t��![]() ��ʱ��DE=AD��AE=5t����3+3t��=2t��3��
��ʱ��DE=AD��AE=5t����3+3t��=2t��3��
����DEG����ACB���ƣ��� ![]() ��
�� ![]() �� ��
�� ��![]() ��
��![]() ��
��
���t=![]() ��t=
��t=![]() ��
��
������������t=![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ʱ����DEG����ACB���ƣ�
ʱ����DEG����ACB���ƣ�

 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�����Ŀ��ij�߲˹�˾�չ��߲˽������۵Ļ���������±���ʾ��
���۷�ʽ | ֱ������ | �ּӹ������� | ���ӹ������� |
ÿ�ֻ���/Ԫ | 100 | 250 | 450 |
���ڸù�˾�չ���140���߲ˣ���֪�ù�˾ÿ���ܾ��ӹ��߲�6�ֻ�ּӹ��߲�16�֣����ּӹ�����ͬʱ���У���
��1�����Ҫ����18����ȫ����������140���߲ˣ���������б���
���۷�ʽ | ȫ��ֱ������ | ȫ���ּӹ����� | �������ӹ���ʣ �ಿ��ֱ������ |
����/Ԫ |
��2������Ƚ��о��ӹ���Ȼ����дּӹ���Ҫ����15���ڸպüӹ���140���߲ˣ���Ӧ��η���ӹ�ʱ�䣿
��3�����Ҫ���߲˶�Ҫ�ӹ������ۣ��ҹ�˾������������42200Ԫ���ʣ����ٽ����ٶ��߲˽��о��ӹ���