题目内容
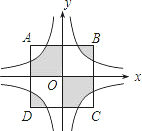 正方形ABCD的顶点A(2,2),B (-2,2),C (-2,-2),反比例函数y=
正方形ABCD的顶点A(2,2),B (-2,2),C (-2,-2),反比例函数y=| 2 |
| x |
| 2 |
| x |
| A、2 | B、4 | C、6 | D、8 |
考点:反比例函数图象的对称性
专题:
分析:先根据两反比例函数的解析式确定出两函数图象之间的关系,再根据正方形ABCD的对称中心是坐标原点O可知图中四个小正方形全等,反比例函数的图象与两坐标轴所围成的图形全等,故阴影部分的面积即为两个小正方形即大正方形面积的一半.
解答:解:由两函数的解析可知:两函数的图象关于x轴对称.
∵正方形ABCD的对称中心是坐标原点O,
∴四个小正方形全等,每个小正方形的面积=
S正方形ABCD=
×4×4=4,
∴反比例函数的图象与两坐标轴所围成的图形全等,
∴阴影部分的面积=
S正方形ABCD=
×4×4=8.
故选:D.
∵正方形ABCD的对称中心是坐标原点O,
∴四个小正方形全等,每个小正方形的面积=
| 1 |
| 4 |
| 1 |
| 4 |
∴反比例函数的图象与两坐标轴所围成的图形全等,
∴阴影部分的面积=
| 1 |
| 2 |
| 1 |
| 2 |
故选:D.
点评:本题考查的是关于x轴对称的反比例函数解析式的特点,解答此题的关键是根据函数解析式判断出两函数图象的特点,再根据正方形的面积即可解答.

练习册系列答案
相关题目
在Rt△ABC中,a,b,c为△ABC三边长,则下列关系正确的是( )
| A、a2+b2=c2 |
| B、a2+c2=b2 |
| C、b2+c2=a2 |
| D、以上关系都有可能 |
某中学生暑期环保小组的同学,随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量,数据如下:6,5,7,8,7,5,8,10,5,9(单位:个).利用这些数据估计该小区2 000户家庭一周内需要环保方便袋约( )
| A、2 000个 |
| B、14 000个 |
| C、21 000个 |
| D、98 000个 |
 将一个矩形的纸对折两次,沿图中虚线将一角剪掉再打开后,得到的图形为( )
将一个矩形的纸对折两次,沿图中虚线将一角剪掉再打开后,得到的图形为( )A、 |
B、 |
C、 |
D、 |
下列运算正确的是( )
A、
| ||||||
B、3
| ||||||
C、2+
| ||||||
D、a
|
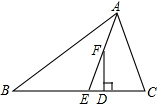 如图,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上的一点,且FD⊥BC于D,则∠EFD与∠B,∠C的关系是
如图,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上的一点,且FD⊥BC于D,则∠EFD与∠B,∠C的关系是