Question

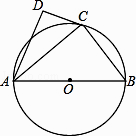
【题目】如图，点C、E分别为△ABD的边BD、AB上两点，且AE=AD，CE=CD，∠D=70゜，∠ECD=150゜，求∠B的度数．

Answer 1

【答案】见解析

【解析】

试题连结AC，证△ACE≌△ACD(SSS)，∠AEC=∠D="70°," ∠BEC="110°," ∠ECB=180-150=30°

所以∠B=180-110-30=40.

试题解析：解:连接AC；

因为，在△ACE和△ACD中，AE =" AD" ，CE =" CD" ，AC为公共边，

所以，△ACE ≌ △ACD ，

可得：∠AEC = ∠ADC =" 70°" ，

所以，∠B = ∠AEC-∠BCE = ∠AEC-(180°-∠ECD)

= 70°-(180°-150°)

= 40°.