题目内容
【题目】已知:如图所示,点E在直线DF上,点B在直线AC上,∠A=50°,∠AGB=∠EHF,∠C=∠D,求∠F的度数.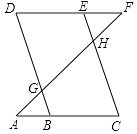
【答案】解:∵∠AGB=∠EHF,∠AGB=∠DGF,
∴∠DGF=∠EHF,
∴BD∥CE,
∴∠C=∠ABD;
又∵∠C=∠D,
∴∠ABD=∠D,
∴AC∥DF,
∴∠F=∠A=50°
【解析】由∠AGB=∠EHF可分别转化为其对顶角,证得BD∥CE,推出∠C=∠ABD,再由已知推得AC∥DF,进而∠F=∠A=50°.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

练习册系列答案
相关题目