题目内容
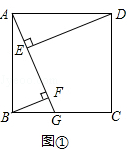
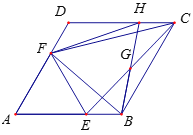
【题目】如图，在菱形ABCD中，
．点E、F分别是边AB、AD上的点，且满足
，连结EF．
（1）求证: 
为等腰三角形；
（2）若
，求
的面积；
（3）若G是CE的中点，连结BG并延长交DC于点H，连结FH，求证：
.
【答案】(1)证明见解析；(2)
；（3）证明见解析.
【解析】(1)根据菱形的性质得到
，
，然后根据全等三角形的判定AAS证得
≌
，进而根据全等三角形的性质和等腰三角形的判定得证结论；
(2)根据（1）的结论得到
，从而根据菱形的领边相等得到△AEF是等边三角形，求得AE=AF=2，作
于点M，根据30°角的直角三角形的性质和勾股定理求出FM的长，求得三角形的面积；
（3）根据全等三角形的判定ASA证得
≌
，然后根据全等三角形的性质得到
，，进而得到
，即
.
(1)证明：∵四边形
为菱形
∴，
在和中
∴≌（AAS）
∴
∴
为等腰三角形.
(2)∵≌
∴
∵
∴
又∵
∴
为等边三角形
∴
作于点M
∴
∴
∴
∴
.
（3）∵G是
中点
∴
∵
∴
在和中
≌（ASA）
∴
由（1）知：≌
∴
∵
，
∴
又∵
∴
又∵
∴
∴
∴.
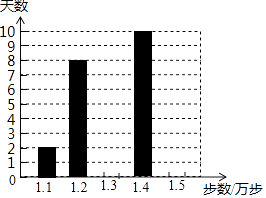
名校课堂系列答案
【题目】小明骑自行车去学校，最初以某一速度匀速行驶，中途自行车发生故障，停下来修车耽误了几分钟，为了按时到校，他加快了速度，仍保持匀速行驶，结果准时到校，到校后，小明画了自行车行进路程s(km)与行进时间t(h)的图象，如图所示，请回答：
(1)这个图象反映了哪两个变量之间的关系？
(2)根据图象填表：
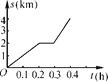
时间t/h | 0 | 0.2 | 0.3 | 0.4 |
路程s/km |
(3)路程s可以看成时间t的函数吗？
【题目】新年晚会，是我们最欢乐的时候.会场上，悬挂着五彩缤纷的小装饰，其中有各种各样的立体图形，如图所示.
(1)数一下每一个多面体具有的顶点数
、棱数
和面数
.并且把结果记入表中.
多面体 | 顶点数 | 面数 | 棱数 |
正四面体 | 4 | 4 | 6 |
正方体 | |||
正八面体 | |||
正十二面体 | |||
正二十面体 | 12 | 20 | 30 |
(2)观察表中数据，猜想多面体的顶点数、棱数和面数之间的关系.
(3)伟大的数学家欧拉(Euler,1707-1783)证明了这一令人惊叹的关系式，即欧拉公式.若已知一个多面体的顶点数=196，棱数=294.请你用欧拉公式求这个多面体的面数.
